The exact solution [i.e. finding analytic equations for thermodynamic properties for a model Hamiltionian] by Andrei and Wiegmann in 1980 was a remarkable and unanticipated achievement. First, it showed that the "solution" of the Kondo problem in the 1970s via numerical renormalisation group and Fermi liquid approaches was correct. Second, it gave analytic formula for thermodynamic properties in weak and strong magnetic fields. Third, it gave an explicit form for the scaling function for the specific heat over the full temperature range.
On the more mathematical side it was of interest because it used Bethe ansatz techniques previously used for quite different one dimensional lattice models (Heisenberg, Hubbard, Bose gas with delta function repulsion, ice-type....). This may have also stimulated the connection of the Kondo problem to boundary conformal field theory pioneered by Affleck and Ludwig around 1990.
Calculation of the Wilson number was one impressive result which really helped convince people that the Bethe ansatz solution was correct. This dimensionless ratio connects the Kondo energy scale at high and low energies, as discussed in my earlier post summarising chapter 4.
First, it is worth remembering the amazing fact that everything is universal and there is only ONE energy scale, the Kondo temperature.
Second, note how slowly one approaches the high energy limit where the impurity spin is decoupled from the conduction electrons. This is due to logarithmic terms. Even when the temperature or field is several orders of magnitude larger than the Kondo temperaure the effective moment of the impurity is still of order only 90 per cent of its non-interacting value.
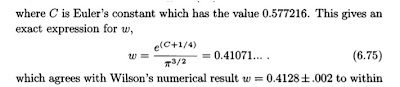






No comments:
Post a Comment