There is a nice paper
by Giovanni Sordi, Patrick Sémon, Kristjan Haule, and Andre-Marie Tremblay
The abstract ends with the important and articulate claim:
Broken symmetry states appear in the pseudogap and not the other way around.
The figure below shows the phase diagram that the authors calculated for the doped Hubbard model with cluster DMFT. The key point is that at low temperatures there is a first-order phase transition from the pseudogap to a correlated Fermi liquid. Furthermore, there is no symmetry breaking associated with this transition. In this respect the phase diagram is analogous to a liquid-vapour transition in a simple fluid and so the authors identify the metal-pseudogap crossover line with the Widom line for the former class of transitions.
This is an elegant new idea.
In the actual materials this first-order transition is masked by the presence of superconductivity.
Surely, this means that in high magnetic fields, which destroy the superconductivity, one should see this transition. In a single material (i.e. fixed doping) observing this may be a little tricky, requiring the first-order line to have a negative slope, and extremely high magnetic fields.
Another really nice and interesting result is connecting the pseudogap to fluctuating RVB type singlets. The figure below shows the temperature dependence of the probability of finding a singlet state on a single plaquette. [See earlier post one and two on how these RVB states appear in four-site Heisenberg models.]
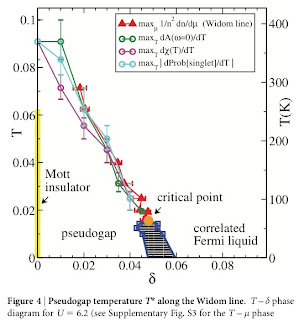
Another question concerns what happens in the half-filled Hubbard model and the organic charge transfer salts. Figure 4 of an earlier PRL by the same authors gives a more general phase diagram (temperature vs. doping and U/t). I am not quite sure how to decode it and connect it to the organics and the bandwidth driven Mott transition that occurs at half-filling.




That paper has been out for a long time. It's pretty old new to the alert and attentive.
ReplyDeleteI'd rather you comment on this.
It's pretty embarrassing to the field as a whole in my honest opinion.
Hi Ross,
ReplyDeleteThank you very much for your useful comments related to our paper on the Widom line and the pseudogap. You end on a question concerning http://prl.aps.org/abstract/PRL/v108/i21/e216401 . "Figure 4 of an earlier PRL by the same authors gives a more general phase diagram (temperature vs. doping and U/t). I am not quite sure how to decode it and connect it to the organics and the bandwidth driven Mott transition that occurs at half-filling." That figure shows that superconductivity near the bandwidth-driven Mott transition is continuously connected to superconductivity appearing in the doping driven transition. There however, the calculation is for the square lattice. For the organics, we would need to do the same problem on the anisotropic triangular lattice. We already know from CDMFT at T=0 that there is a superconducting phase adjacent to the bandwidth driven transition http://prl.aps.org/abstract/PRL/v97/i4/e046402 . One can guess that as a function of doping something similar will occur. We have preliminary results on this. But this remains to be checked more thoroughly.