Caveats about thermopower interpretation

The thermoelectric power of a metal is rather complex. Even Ashcroft and Mermin suggested that it was difficult to interpret and relate to the theoretical calculations.
Earlier posts have considered some of the subtleties, particularly in strongly correlated electron systems.

To me a couple of recent experimental papers present beautiful data but are not cautious enough in their interpretation. They need to rule out alternative explanations [see below] before I will be convinced of the explanations that they propose.

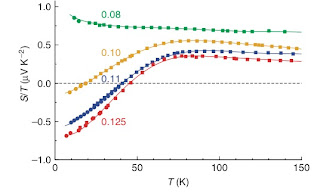
Fermi-surface reconstruction by stripe order in cuprate superconductors
F. Laliberté, J. Chang, N. Doiron-Leyraud, E. Hassinger, R. Daou, M. Rondeau, B.J. Ramshaw, R. Liang,  D.A. Bonn, W.N. Hardy, S. Pyon, T. Takayama, H. Takagi, I. Sheikin, L. Malone, C. Proust, K. Behnia, and Louis Taillefer

They observe a sign change in the thermopower and associate this with a Fermi surface reconstruction, stripe formation, and a quantum phase transition.

Spin fluctuation driven enhancement of thermopower near the quantum critical point in Ba(Fe(1-x)Co(x))2As2

S. Arsenijević, H. Hodovanets, R. Gaál, L. Forró, S. L. Bud'ko, P. C. Canfield

In both papers, the fact that S/T for a specific doping has a logarithmic temperature dependence over about a decade in temperature is equated with quantum criticality.

Why am I not convinced?

1. A recent preprint shows the cuprate data can be explained using the semi-classical Boltzmann equation and a Functional Renormalisation Group treatment of the Hubbard model (see Figure 10). The sign change is associated with a the van Hove singularity and a Lifshitz transition.

2. Dynamical mean-field theory (DMFT) shows how the thermopower can change sign as a function of temperature due to strong correlations and the associated low coherence temperatures. (See e.g. Figure 4 in this preprint which I discussed in an earlier post).

I suspect that a DMFT treatment of the relevant multi-band Hubbard model with Hund's rule coupling [a la Park, Haule, Kotliar] will be able to explain the thermopower data for the pnictides.