There is a nice review Numerical studies of the 2D Hubbard model by Doug Scalapino which considers the question.
He claims that in the end the answer is yes.
However, there are several subtleties along the way. I just mention two that I learnt.
To attempt to answer the question one calculates the d-wave pairing susceptibility on a finite lattice.
Puzzle/caution/subtlety I
the pairing susceptibility is less than for U=0!
Clearly there is no superconductivity for U=0 and a key claim of the Anderson paradigm is that large U and correlations are the key for high-Tc. So what is going on?
Scalapino and his collaborators argue that this decrease with increasing U is because U reduces the single particle spectral weight [i.e. the effective mass of quasi-particles increases with increasing U] and so P_d should be compared to the function below which is the value of P_d in the absence of interactions between the holes.
Puzzle/caution/subtlety II
finite size effects and dependence on cluster geometry
It turns out that the results don't just depend on the size of the cluster but also its geometry. "One needs to take into account the 4-site local plaquette structure of the order parameter." Z_d is the number of independent near-neighbour plaquettes on a cluster. For the square 16 site cluster (16B) in the figure below Z_d=2. In contrast, for the diamond 16 site cluster (16A) on has Z_d=3. As a result the pairing correlations are suppressed in 16A relative to 16B.
Getting or not getting superconductivity in quantum Monte simulations is certainly subtle. A different technique [constrained path Monte Carlo and which is at zero temperature] used by a different group did not produce long range correlations. [See this PRB from 1999]. I am not sure if this discrepancy has ever been explained to the satisfaction of all parties...
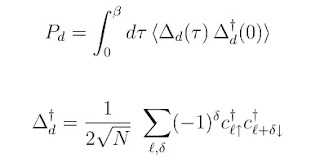
Hi Ross,
ReplyDeleteIn the absence of exact results, we can also be comforted when non-perturbative methods that start from very different points of view give consistent results. For d-wave superconductivity, one finds in Fig. 1 of http://prb.aps.org/abstract/PRB/v68/i17/e174502that at U=4t, Two-Particle-Self-Consistent (TPSC) theory is in agreement with available Quantum Monte Carlo (QMC) results to a few percent accuracy. While QMC cannot go to low temperature because of the sign problem, TPSC can. One then finds Tc=0.029 at the 10% doping considered in the DCA paper you quote, where Tc=0.023. TPSC satisfies the Mermin-Wagner theorem, Pauli principle and some exact sum-rules.
One can verify within TPSC why the U=0 value of the pair-susceptibility is larger than the interacting one at large temperature where determinantal QMC is available. If you do not take vertex corrections into account, the pseudogap removes states at the Fermi level and the interacting pair-susceptibility (bubble) is smaller than the U=0 one.
At U=4t, t'=0, the dome shape of Tc comes from the same physics. While the vertex corrections from AFM interactions increase as you approach half-filling, the pseudogap overcompensates and makes Tc go down. Fig. 3 of the above paper illustrates this. This is in agreement with the Scalapino explanation.
Hi Andre-Marie,
ReplyDeleteThanks. This is very helpful.