Is there superconductivity in the Hubbard model?

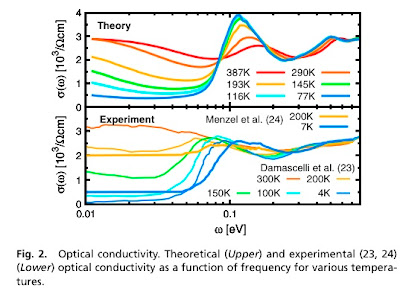
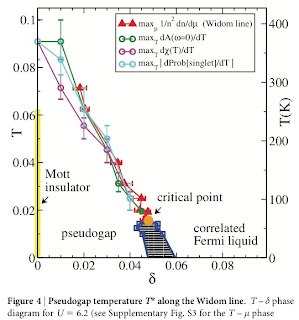
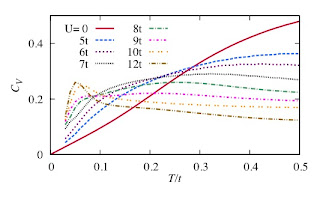
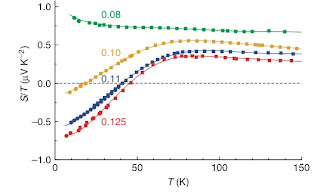
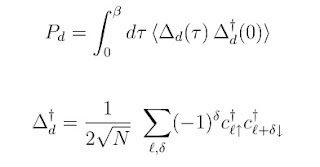Previously, I considered the tricky problem of Does the doped Hubbard model superconductor?
I mentioned in passing a worrying quantum Monte Carlo study published in PRB in 1999

Correlated wave functions and the absence of long-range order in numerical studies of the Hubbard model
M. Guerrero, G. Ortiz, and J. E. Gubernatis

The graph below shows the distance dependence of the pairing correlation function in the d-wave channel. If superconductivity occurs it should lend to a non-zero value equal to the square of the superconducting order parameter.
It certainly looks like it tends to zero at large distances.

However, careful examination shows that it seems to have a non-zero value of order 0.001.
Perhaps, that is just a finite size effect.
But, we should ask, "How big do we expect the long-range correlations, i.e. the magnitude of the square of the order parameter d, to be?"

A cluster DMFT calculation on the doped Hubbard model (in the PRB below) gives a value of order 0.03 for the order parameter d. This means d^2 ~ 0.001 consistent with the QMC study which claims no superconductivity!

Anomalous superconductivity and its competition with antiferromagnetism in doped Mott insulators
S. S. Kancharla, B. Kyung, D. Sénéchal, M. Civelli, M. Capone, G. Kotliar, and A.-M. S. Tremblay

Similar issues arise when assessing the results of
Absence of Superconductivity in the Half-Filled Band Hubbard Model on the Anisotropic Triangular Lattice
R. T. Clay, H. Li, and S. Mazumdar

If I take the order parameter estimated by a RVB calculation reported in this PRL (by Ben Powell and myself) and square its value it predicts a long-range pairing correlation (~0.001) comparable to the extremely small values found in the numerical study claiming absence of superconductivity.

Clay, Li, and Mazumdar also mentioned the problematic observation that the pairing correlation they calculated did not increase with the Hubbard U. However, my previous post discussed how Scalapino and collaborators argued this is because one needs to factor in the quasi-particle renormalisation Z that also occurs with increasing U. For the half-filled Hubbard model this probably leads to an order of magnitude enhancement of the pairing as U increases towards the Mott insulating phase, since Z decreases from 1 to 0.3 and the renormalised P_d scales with 1/Z^2.

So, I remain to be convinced that superconductivity does not occur in the Hubbard model, both upon doping the Mott insulator or at half-filling near the band-width controlled Mott transition.

Impact factors have no impact on me

There seems to be a common view that on CVs (and grant applications) people should list the Impact Factors for each journal in which they have a paper.
To me this "information" is just noise and clutter.
I do not include it in my own CV or grant applications.
Why?

1. IFs just encode something I know already.
Nature > Science > PRL ~ JACS > Phys. Rev B ~ J. Chem. Phys. > Physica B ~ Int. J. Mod. Phys. B > Proceedings of the Royal Society of Queensland .....

2. There is a large random element in success or failure to get an individual paper published in a high profile journal. e.g., who the referees are.

3. The average citations of a journal is not a good measure of the significance of a specific paper. There is a large variance. What really matters is how much YOUR/MY specific paper in that journal is cited in the long term. Unfortunately, in most cases it is hard to know in less than 3-5 years.

4. Crap papers can get published in Nature and Science. Hendrik Schon published almost 20 papers in Nature and Science. On the other hand, Nobel Prize winning papers are sometimes published in Phys. Rev. B (e.g. giant magnetoresistance).

5. I don't need to know the actual IF of a journal with an impact factor of one or less in order to know that it is a rubbish journal. I already know that because I virtually never read papers in such journals simply because they virtually never contain anything that is significant, interesting, or valid. My "random" meanderings through the literature virtually never lead me there.

6. I remain to be convinced that reporting IFs to more than 2 significant figures and without error bars is meaningful.

I fail to see that alternative metrics such as the Eigenfactor resolve the above objections.

The only value I see in IFs is helping librarians compile draft lists of journals to cancel subscriptions to in order to save money.

I am skeptical that IFs are useful for comparing the research performance of people in different fields (e.g. biology vs. civil engineering vs. psychology vs. chemistry).

And in the end... what really matters is whether the paper contains interesting, significant, and valid results... Actually looking as some of an applicant's papers and critically evaluating them is the best "metric". But that requires effort and thought...

What did Wilson do?

Last week we struggled through chapter 4, "Renormalisation group calculations" of Hewson's book, The Kondo Problem to heavy fermions.

The focus is on Kenneth Wilson's numerical treatment of the Kondo problem, mentioned in his Nobel prize citation. Much of it still remains a mystery to me...
Here are a few key aspects. Please correct me where I am wrong or at least confused...

First, he mapped the three-dimensional Kondo model Hamiltonian into a one dimensional tight binding chain (half-line) with single impurity spin at the boundary. This simplification makes the problem more numerically tractable.

Next, he used a logarithmic discretization (in energy) of the states in the conduction band. This important step is motivated by the logarithmic divergences found by Kondo's perturbative calculation and Anderson's poor man's scaling arguments.

He then numerically diagonalises the Hamiltonian with a discrete set of states for a finite chain. One then rescales the Hamiltonian, truncates the Hilbert space, and adds an extra lattice site.

Eventually, one converges to the strong coupling fixed point and one observes an almost equally spaced excitation spectrum, characteristic of a Fermi liquid.

A surprising thing is that the rescaling parameter Lambda is set to a relatively large value of 2, compared to a value close to one, that one might expect to be needed. Wilson was clever to realise/find that such coarse graining would work so well.

Wilson extracted a large amount of information from his calculations. Here are a few important findings.

1. The impurity specific heat and impurity susceptibility had a Fermi liquid temperature dependence. The latter was given by

[This] shows that there is no residual local moment, and that the impurity spin is fully compensated. The numerical factor 0.4128 is a universal number for the s-d model, and is known as the Wilson number, w. It relates two quite different energy scales for the s-d model, T_K, which is determined from the high temperature perturbative regime, and chi_imp(0), the low temperature susceptibility associated with the strong coupling regime.

2. The Sommerfeld-(Wilson) ratio had a universal value

3. Over an intermediate temperature range (one and half decades) the temperature dependence can be fit to

This Curie- Weiss form corresponds to a reduced moment compared to the free spin form. Thus the impurity moment, even for T ~ T_K, is only of the order of 30% that of the free moment. The residual effects of the screening of the conduction [electrons] persist to very high temperatures because of the logarithmic dependence on T/T_K.

4.  The complete universal dependence with a logarithmic temperature scale is shown below

Writing effective papers

Weston Borden's article 40 years of fruitful chemical collaborations has an significant observation concerning writing effective papers: focus on the physical explanation of the results rather than on the details of the methodology.
He recounts how he he learnt this, while starting out as an Assistant Professor at Harvard, in a collaboration with Lionel Salem. Borden had performed some calculations using the Pariser-Parr-Pople (PPP) model for the electronic structure of conjugated organic molecules [for physicists an extended Hubbard model with long-range Coulomb interactions].

Lionel read my draft, and he promptly rewrote it. Lionel’s revised version, which was the one that we published, focused much more than my draft had on the explanation of the PPP results, rather than on the details of the calculations. This experience taught me a valuable lesson. Although describing the details of calculations and the results obtained from them is certainly important, it is even more important to write a clear, physical explanation of the results. 

This was also the lesson that I learned from the papers that Roald Hoffmann published in the late 1960s and early 1970s. Although it was well-known that the Extended Hückel (EH) method that Roald used was quantitatively unreliable, Roald provided such convincing qualitative explanations of his EH results that it always seemed to me Roald’s EH results must be correct.

I think these observations are just as relevant and important for physicists.

Aside: an earlier post sung the praises of Hoffmann's paper titles.

Borden then makes the important and worrying observation:

Perhaps the tremendous increase in the accuracy of electronic structure calculations during the past 40 years has had the undesirable consequence that computational chemists feel less obliged to provide the kind of detailed physical explanations of their results than Roald routinely furnished 40 years ago.

Transition from a band insulator to a bad metal

Many previous posts have considered how in a metallic phase close to a Mott insulator one can observe a crossover from a Fermi liquid to a bad metal with increasing temperature.

One observes something quite different in FeSi (iron silicide) which has been a subject of debate for several decades. Different paper titles include the following words: Kondo insulator, ferromagnetic semiconductor, unconventional charge gap, strong electron-phonon coupling, Anderson-Mott localization, singlet semiconductor, covalent insulator, correlated band insulator, ferromagnetic metal, ....

At low temperatures FeSi is a semiconductor with a gap of about 50 meV (500 K). Both the spin susceptibility and the resistivity are gapped. However,  around 200 K there is a crossover to a bad metal.
The spin susceptibility has a maximum versus temperature around 400 K and above that can be fitted to a Curie-Weiss form, suggesting the presence of local moments.
The thermopower has a maximum around 50 K with a colossal value of 700 microVolts/Kelvin, making the material attractive for thermoelectric applications. The thermopower changes sign at about 150 K and 200 K.
With increasing temperature the optical conductivity shows redistribution of spectral weight on the electron Volt (eV) scale, an important signature of strong electronic correlations.

There is a really nice paper which provides a compelling theoretical description and explanation of what is going on.
Signatures of electronic correlations in iron silicide
Jan Tomczak, Kristjan Haule, and Gabi Kotliar

The authors perform electronic structure calculations combining Density Functional Theory (DFT) [at the level of Generalised Gradient Approximation (GGA)] with DMFT [Dynamical Mean-Field Theory].
They reproduce the main features of the experimental data.

Here is some of the key physics.
FeSi is a band insulator at low temperatures.
With increasing temperature there is a crossover to incoherence, i.e. the Bloch wavevector is no longer a good quantum number.
Fe is in a mixed valence state with a mean valence (no. of d electrons) of 6.2 and a variance of 0.9.
There is a preponderance of S=1 states, contrary to earlier suggestions that FeSi is a singlet insulator.
The incoherence arises because of fluctuations in the local moment, which is to a large extent non-local.
The results are controlled by the Hund's coupling J rather than the Hubbard U, something also seen recently in other systems with orbital degeneracy [see this two-faced post or discussion of strontium ruthenate or a recent review].

40 years of collaborative quantum chemistry

There is a very nice article in the Journal of Organic Chemistry
With a Little Help from My Friends: Forty Years of Fruitful Chemical Collaborations
by Weston Thatcher Borden

Borden's career is unusual in that he has done both organic synthesis [i.e., actually making molecules] and computational quantum chemistry.

The article is worth reading for several reasons. It describes some
-interesting organic chemistry and shows how quantum chemistry has illuminated it
-characteristics of fruitful collaborations, both between theorists and between theorists and experimentalists
-interesting history and personal vignettes and perspectives

On the latter I found the following throwaway line rather disturbing and disappointing:

When I was an Assistant Professor at Harvard, unlike most of my colleagues in the Chemistry Department, Bill Doering seemed genuinely interested in talking about chemistry with me.

Unfortunately, this happens too often. I would be curious to know why Borden thinks this was. Sometimes it is because people are too "busy" and/or preoccupied with their own little world. The worst reason can be senior scientists actually lose interest in science and get consumed with funding, politics, ...alternatives to struggling to do significant research.

Some of the insights in the article justify a blog post in their own right and so I hope I will post separately about writing up quantum chemistry calculations, tunneling by carbon in organic reactions, symmetry breaking in TMM, and "different electronic states of the same molecule can have different MOs [Molecular Orbitals],..."

A paper of Borden's featured in an earlier post Seeing how degenerate radicals can be

Topological insulators get more interesting

Topological insulators (TIs) are certainly a hot topic. However, there are two things that might make one nervous about all the excitement.

1. All the materials being studied as TIs [e.g. Bi2Se3] actually aren't TIs.
What!? A TI is by definition a bulk insulator with surface metallic states that are topologically protected. However, the actual materials turn out not to be bulk insulators. On a practical level this makes separating out bulk and surface contributions, particularly in transport measurements, tricky. But, also presents an ideological problem: one is not actually studying the phase of matter one wishes one was studying.

2. One could argue that TIs are "just a band structure effect", i.e., they do not involve any quantum many-body physics.

However, these objections are put to rest by a preprint
Discovery of the First True Three-Dimensional Topological Insulator: Samarium Hexaboride
Steven Wolgast, Cagliyan Kurdak, Kai Sun, J. W. Allen, Dae-Jeong Kim, Zachary Fisk

They report electrical transport measurements that show that SmB6 is a bulk insulator with surface metallic states.
This is of particular interest for several reasons

a. The material really is a true topological insulator.
b. The material is a Kondo insulator. [Although strictly the material is in the mixed valence rather than the local moment regime.] The insulating state emerges from strong electronic correlations.
c.  This resolves long standing puzzles about previous transport measurements on this material which did not show activated conductivity at low temperatures. This can now be explained as a sample dependent contribution from metallic surface states.
d. This material was predicted to be a topological Kondo insulator by Dzero, Sun, Coleman, and Galitski.

I also note a recent paper Actinide Topological Insulator Materials with Strong Interaction.

I thank Tony Wright for bringing the preprint to my attention.

Am I missing something?

There is a paper in Science this week Flows of Research Manuscripts Among Scientific Journals Reveal Hidden Submission Patterns

The authors claim, 

Resubmissions were significantly more cited than first-intents published the same year in the same journal.... 

... these results should help authors endure the frustration associated with long resubmission processes and encourage them to take the challenge 

Then I looked at the data below to see how strong the claimed effect was.

I think the horizontal lines mark the mean and the box shows the variance.
Hence, it looks to me like citations may increase by less than 10% with resubmission.

This hardly seems on any significance to me.
But, am I missing something?

Maybe this is another issue of comparisons are in the eye of the beholder or the silly claims that journals make about their impact factors or some faculty make about their student evaluations.

The wealth of a poor man's scaling

Chapter 3 of Hewson's The Kondo Problem to Heavy fermions reviews Anderson's poor man's scaling treatment of the Kondo model.

Starting with the anisotropic Kondo Hamiltonian

one rescales the electronic bandwidth D and see how the interactions J_z and J_ and J+ rescale.

To lowest order in perturbation theory this leads to the renormalisation group equations

Solving these gives the flow diagram below

A few important consequences

1. Antiferromagnetic (AFM) interactions flow to strong coupling.

2. The Kondo energy/temperature is invariant to the flow.

3. This is an example of asymptotic freedom [interactions can weaker at higher energies].

It is impressive that Anderson did this before Wilson and Fisher used renormalisation group ideas to describe critical phenomena in classical phase transitions.

It is fascinating that the same flow equations and flows describe the Kosterlitz-Thouless phase transition associated with topological order [vortex pair unbinding] in a classical two dimensional superfluid.

The spin boson model which describes the quantum decoherence of a single qubit in an ohmic environment can be mapped to the anisotropic Kondo model and so is also described by the same flow equations [See this famous (and rather dense) review by Leggett et al.]

17 citations in 12 years in not impressive

I can fully imagine a grant reviewer, tenure or hiring committee saying that when reviewing the "impact" of a particular publication of an individual.

Furthermore, one can also say
"the paper was in PRL but it was a full 12 months between submission and publication. Clearly, he was lucky to get in PRL at all..."

But, there is a problem with all this.
These observations apply to Duncan Haldane's 1988 paper Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the "Parity Anomaly"

Haldane's paper has been receiving about 100 citations per year for the past few years.
It now has a total of 530 citations in Physical Review journals.
However, from 1988 to 1999 it received only 17 citations.
Hardly impressive.

The Kondo effect is non-perturbative

Last week we read "Beyond perturbation theory", chapter 3 of Hewson's The Kondo Problem to Heavy Fermions.

First he gives, without derivation, perturbation expressions for the impurity spin susceptibility and specific heat. The results exhibit logarithmic divergences at temperatures of the order of the Kondo temperature.

Hewson discusses some of the herculean efforts in the 1960s of people such as Abrikosov, Suhl, and Hamann, to come up with new diagrammatic techniques and summations to get rid of, or at least reduce, the divergences.
The results still have logarithmic temperature dependences. None give the Fermi liquid like dependences at low temperatures that experiments hinted at.

The Kondo effect is non-perturbative. n.b. the Kondo temperature has a non-analytic dependence on J.

What does one do?
An important insight was variational wave function proposed by Yosida in 1966.

One finds that the ground state is a spin singlet between the impurity spin and a superposition of the electrons above the Fermi sea. The binding energy has a similar non-analytic dependence on J as the Kondo temperature. Indeed if the wave function is generalised to include an infinite number of particle-hole pair excitations one finds that the binding energy is the Kondo temperature. Furthermore, the spin susceptibility is finite and inversely proportional to the Kondo temperature.

How can one describe the crossover with temperature to formation of these Kondo singlets and the emergence of the Kondo energy scale?
Anderson's poor mans scaling does that. Since it is such a profound and monumental achievement it deserves a separate post!

Postdoc in theoretical chemical physics at UQ

Seth Olsen and I are about to advertise for a postdoc to work with us at UQ. The flavour of our interests and approach can be seen in posts on this blog under labels such as organic photonics, quantum chemistry, conical intersections, and Born-Oppenheimer approximation.

A draft of the official position description is here. We anticipate an official advertisement will appear shortly. Please contact us if you are interested.

Should I change jobs?

Some of my colleagues, may say "Yes!".
However, this post is mostly concerned with moving from academia to industry and is mostly directed at graduate students and postdocs. However, some of the issues are also relevant to faculty considering a change of institution.
The issues are based on my limited experience and observations over almost three decades. I stress that I am not saying that all the realities below are right or just, only that they are realities that may need to be faced.

Its personal.
Different people have different values.
How much do you value (or don't value) independence, freedom, money, family time, flexible work hours, job "security", affirmation, geographic location, ....?
The relative value you place on such things will significantly affect what job may be suitable for you and whether and when you decide to make a change?
A job that is great for your friend may be horrible for you and visa versa.
There is no simple right answer.

Every job sucks.
or at least some of it sucks...
Read Genesis 3 and Ecclesiastes. Earning a living is tough.
The grass usually looks greener elsewhere. Stop looking for the perfect job.
Unfortunately, every job involves some frustration, some instability, some inane policies, some tedious tasks, some insufferable colleagues, some anxiety, some incompetence, some compromise, limited appreciation, and limited resources....
I concede these problems are greater in some jobs than others. However, I think they are pretty significant in any job and any institution.
The quicker you come to terms with this painful reality and learn how to cope with these challenges the greater your job satisfaction will be and may save you from making a change that just dishes up the same (or a new set) of frustrations and disappointments.

Most science and humanities Ph.D's will not get permanent jobs in academia.
Consider the brutal statistics: the number of Ph.D graduates every year vastly outnumbers the number of faculty positions. It has been that way since the 1970s and will continue to be so. Don't believe anyone who tells you otherwise.  Nevertheless, I am still pleasantly surprised at the number of people I encounter who do seem to stick at it and somehow survive, particularly with some luck, and if they are geographically flexible.

There are many intellectually challenging jobs outside academia.
If you leave, either because you have to or decide to, you have not "failed" in any sense and are not destined to intellectual mediocrity. After all, there are "brain dead" jobs both inside and outside academia. Don't let anyone look down on you.

Deal with your inner demons first.
Anxiety, difficulty getting along with colleagues, disappointment, stress, perfectionism, yearning for affirmation and appreciation, poor self-esteem, lack of confidence, lack of contentment, depression....
Don't think changing jobs is going to make these personal issues go away. They may be less acute in some jobs but they will still be there. They may be even be more acute in industry. Don't let a desire to escape these pressures drive a decision.
I wish I had dealt with such issues earlier in my career.

You may not make more money in industry than in academia.
It is certainly true that some gifted and fortunate individuals make a ton of money in industry. The former Chief Scientist of Queensland was fond of telling science students that many of the richest people in the world had science or engineering degrees. However, you are probably not going to be one of them.
It may be true that the average starting salary for a science Ph.D in industry is much greater than a postdoc salary, even some junior faculty salaries.
However, do not assume that in industry that you will make this much money (plus more) every year of your life until retirement. 
Hiring and firing, boom and bust: that is the natural cycle of high-flying industry.
I have known people who have had very high paid jobs in industry for a few years, followed by periods of unemployment or under-employment. Sometimes they have also been forced to undergo costly relocations to stay employed.
Also factor in the high cost of living [or very long commutes] that may go with high paid jobs in locations such as London, New York City, or Palo Alto.

Make a decision. Then stick to it for a definite period of time.
Will I? Won't I?
If for an extended period of time you are constantly uncertain and wanting to regularly discuss it with your family, friends, and/or colleagues it may not only drive you crazy but also them.

During a possible transition out of academia be circumspect about who you confide in
If you let many people know you are really uncertain about trying to stay in academia you may find that the commitment, interest, and support of some funding agencies, colleagues, collaborators, supervisors, grant assessors, and/or mentors will fade or vanish. Why should they invest scarce time or resources in you if you may disappear soon? You may then no longer have the option of staying.

Finally don't let uncertainty and anxiety about the future spoil your enjoyment of the present.
Doing good science should be a fun and is a privilege. Try and enjoy it, even if you may not get to do it in the long term.

I welcome discussion. It would be particularly good to hear some first or second-hand experiences of people who have made the transition from academia to industry.

Pseudogap in organic charge transfer salts

This post follows up on earlier posts including
Connecting the pseudogap to superconductivity in the organics

There is a nice paper
Pseudogap and Fermi arc in κ-type organic superconductors
by Jing Kang, Shun-Li Yu, Tao Xiang, and Jian-Xin Li

They use Cluster Perturbation Theory to study the Hubbard model on the anisotropic triangular lattice at half filling. They calculate the one-electron spectral function using clusters as large as 12 sites [embedded self-consistently in an infinite lattice].

The authors find three distinct phases: Mott insulator, Fermi liquid, and a pseudogap state with Fermi arcs. The latter occurs in between the two other phases.

The Figure below shows an intensity map of the spectral function at the Fermi energy for U=4t and t'=0.7t. This clearly shows a complete Fermi surface (with hot spots).

As U increases towards the Mott phase, U=5t one sees parts of the Fermi surface gap out leaving Fermi arcs. Note the cold spots [red region=low scattering=large spectral density] occur at the same place as the nodes in the superconducting gap.

This is quite reminiscent of the physics that occurs in the cuprates and the doped Hubbard model.

What did Kondo do?

Chapter 2 of Alex Hewson's The Kondo problem to heavy fermions reviews what Kondo actually did to get his name on the problem. Here is a brief summary of the highlights from last weeks reading group.

He considered the experimental data on the temperature dependence of the resistivity of metals containing magnetic impurity atoms. It was particularly puzzling that there was a minimum. Generally, one expects scattering (and thus resistivity) to increase with increasing temperature.

First, Kondo recognised that the experimental data suggested that it was a single impurity problem, i.e, one could neglect interactions between the impurities.
Second, the effect seemed to scale with magnitude of the local magnetic moments.
This led him to consider the simplest possible model Hamiltonian the s-d model proposed by Zener in 1951, but now known as the Kondo model.

According to Boltzmann/Drude/Kubo at low temperatures the resistivity of a metal is proportional to the rate at which electrons with momentum k are elastically scattered into different states with momentum k'

Here T_kk' is the scattering T matrix.
Considering Feynman diagrams to second order in J, Kondo showed

One then substitutes this in the formula for the conductivity.

Integrating over energy leads to the famous logarithmic temperature dependence.

I am not really clear on what the essential physics is that leads to this logarithmic divergence, except something to do with spin flips in the particle-hole continuum above the Fermi energy.

The Kondo problem is that this leads to a logarithmic divergence at low temperatures. This suggests perturbation theory diverges. It also suggests an infinite scattering cross section which violates the unitarity limit. Somehow, this divergence must be cut off at lower temperatures by different physics.

The new physics turns out to be formation of spin singlets between the impurity spin and the conduction electron spins. These are known as Kondo singlets, although it was actually Yosida, Anderson, Nozieres, and Wilson who introduced/developed/showed this idea.

Killing comparisons

It is a natural human tendency to compare oneself to ones peers.
I suggest that this can be quite unhelpful for your mental health and for harmonious relationships.
A natural consequence of such comparisons may be discouragement or hubris depending on your personality.

Grad students and postdocs may compare hours worked, numbers of papers, number of interviews, numbers of invited conference talks, attention from their advisor....

Faculty may compare total funding, size of their latest grant, numbers of students, size of office, speed of promotion, h-index, lab space, ...
This can lead to bitterness and friction.

When I was younger I struggled due to making such comparisons. Mostly they led to unnecessary anxiety and discouragement. Furthermore, with hindsight my "metrics" turned out to be pretty irrelevant indicators of future success [i.e. survival] in science. I never considered luck, perseverance, flexibility, passion, communication and personal skills...

Now I am careful not to make comparisons. I don't think they help anyone.
I urge you not to make comparisons. Your mental health may be much the better for it.

First-order transition into the pseudogap state

There is a nice paper

Pseudogap temperature as a Widom line in doped Mott insulators

by Giovanni Sordi, Patrick Sémon, Kristjan Haule, and Andre-Marie Tremblay

The abstract ends with the important and articulate claim:

Broken symmetry states appear in the pseudogap and not the other way around.

The figure below shows the phase diagram that the authors calculated for the doped Hubbard model with cluster DMFT. The key point is that at low temperatures there is a first-order phase transition from the pseudogap to a correlated Fermi liquid. Furthermore, there is no symmetry breaking associated with this transition. In this respect the phase diagram is analogous to a liquid-vapour transition in a simple fluid and so the authors identify the metal-pseudogap crossover line with the Widom line for the former class of transitions.

This is an elegant new idea.

In the actual materials this first-order transition is masked by the presence of superconductivity.
Surely, this means that in high magnetic fields, which destroy the superconductivity, one should see this transition. In a single material (i.e. fixed doping) observing this may be a little tricky, requiring the first-order line to have a negative slope, and extremely high magnetic fields.

Another really nice and interesting result is connecting the pseudogap to fluctuating RVB type singlets. The figure below shows the temperature dependence of the probability of finding a singlet state on a single plaquette. [See earlier post one and two on how these RVB states appear in four-site Heisenberg models.]

Another question concerns what happens in the half-filled Hubbard model and the organic charge transfer salts. Figure 4 of an earlier PRL by the same authors gives a more general phase diagram (temperature vs. doping and U/t). I am not quite sure how to decode it and connect it to the organics and the bandwidth driven Mott transition that occurs at half-filling.

From RVB theory to parliament

When I was a grad student at Princeton, Phil Anderson had a number of students (Zhou Zou, Ted Hsu, Joe Wheatley, ...) who worked on RVB theory. They all eventually left physics for Wall Street. Phil used to joke that they were all making more money than him!

I just learned that Ted Hsu is now a member of parliament in Canada!
I saw this in an article in Physics Today that raises concerns about changes in funding direction for physics in Canada.
There is also an interview with him on the Physics Today site.

Thermodynamics of a transition between a bad metal and a Mott insulator

Jure Kokalj and I just finished a paper
Thermodynamics of a bad metal-Mott insulator transition in the presence of frustration

We study the temperature dependence of a range of thermodynamic properties (charge susceptibility, specific heat, entropy and spin susceptibility) of the Hubbard model on the anisotropic triangular lattice at half filling by means of the numerical finite-temperature Lanczos method. This Hubbard model describes several important families of superconducting organic charge transfer salts.

The results include

• Clear signatures of a metal-Mott insulator transition in the charge susceptibility.
• The metal-insulator transition can be driven either by increasing interactions or by reducing frustration.
• The metallic phase is characterized by a small charge susceptibility, large entropy, low coherence temperature, large renormalized quasiparticle mass, and large spin susceptibility.
• The coherence temperature corresponds to destruction of quasi-particles and crossover from a Fermi liquid to a bad metal. Our estimate of the temperature is comparable to what is observed in the organics. 
• The local magnetic moment in the metallic phase is large and comparable to the local moment in the insulating phase. This is characteristic of a bad metal.
• Frustration increases the density of low-lying spin excitations in the Mott insulating phase and decreases longer range spin correlations.

Are the iron pnictide superconductors strongly correlated?

Yes. According to a nice review by Yu, Si, Goswami, and Abrahams.

A key piece of the evidence for strong correlations is recent inelastic neutron scattering experiments reported in this Nature Physics paper.
They show that even in the superconducting materials [which are doped from parent Antiferromagnetic compounds] there are sizeable fluctuating magnetic moments. The figure below shows the dynamical spin susceptibility versus energy. For both superconducting and antiferromagnetic materials the susceptibility is essentially the same for energies above 100 meV.

The area under the curve is equal to the square of the fluctuating local moment. The magnitude is a few Bohr magnetons, as one would expect in a doped Mott insulator.

Furthermore, a weak coupling RPA treatment [which is invoked to explain the superconductivity] cannot capture the magnitude of these spin fluctuations. In contrast, a DMFT treatment from Park, Haule, and Kotliar is consistent with the experimental data, highlighting the role of strong correlations and Hund's rule coupling.

Caveats about thermopower interpretation

The thermoelectric power of a metal is rather complex. Even Ashcroft and Mermin suggested that it was difficult to interpret and relate to the theoretical calculations.
Earlier posts have considered some of the subtleties, particularly in strongly correlated electron systems.

To me a couple of recent experimental papers present beautiful data but are not cautious enough in their interpretation. They need to rule out alternative explanations [see below] before I will be convinced of the explanations that they propose.

Fermi-surface reconstruction by stripe order in cuprate superconductors
F. Laliberté, J. Chang, N. Doiron-Leyraud, E. Hassinger, R. Daou, M. Rondeau, B.J. Ramshaw, R. Liang,  D.A. Bonn, W.N. Hardy, S. Pyon, T. Takayama, H. Takagi, I. Sheikin, L. Malone, C. Proust, K. Behnia, and Louis Taillefer

They observe a sign change in the thermopower and associate this with a Fermi surface reconstruction, stripe formation, and a quantum phase transition.

Spin fluctuation driven enhancement of thermopower near the quantum critical point in Ba(Fe(1-x)Co(x))2As2

S. Arsenijević, H. Hodovanets, R. Gaál, L. Forró, S. L. Bud'ko, P. C. Canfield

In both papers, the fact that S/T for a specific doping has a logarithmic temperature dependence over about a decade in temperature is equated with quantum criticality.

Why am I not convinced?

1. A recent preprint shows the cuprate data can be explained using the semi-classical Boltzmann equation and a Functional Renormalisation Group treatment of the Hubbard model (see Figure 10). The sign change is associated with a the van Hove singularity and a Lifshitz transition.

2. Dynamical mean-field theory (DMFT) shows how the thermopower can change sign as a function of temperature due to strong correlations and the associated low coherence temperatures. (See e.g. Figure 4 in this preprint which I discussed in an earlier post).

I suspect that a DMFT treatment of the relevant multi-band Hubbard model with Hund's rule coupling [a la Park, Haule, Kotliar] will be able to explain the thermopower data for the pnictides.

Grant application post-mortems (again)

Yesterday the Australian Research Council announced which grant applications were successful for funding for next year. So roughly 20 per cent of people were happy and 80 per cent were sad. After the exhilaration or devastation inevitably come the post-mortems, particularly from those who are unsuccessful. We offer each other a multitude of possible reasons for failure or for success....

Professor Z was on the committee and he doesn't like my field.... All they care about is number of publications.... I need to increase my h-index...  They must have liked the bit I wrote about... Clearly they don't like people who work at the interface of chemistry and physics... I need more Nature papers.... I should have promised less... It is because I did not have a big name person on the grant... it is because I am working on such a hot topic.... Obviously they aren't going to fund 2 groups working in my area.... I think Dr. X must have been that negative referee...People think my group has too much money....

The problem with this type of analysis is that it is all speculation. There is usually NO evidence for any of these ideas. Most funding decisions involve a black box. Input is your application which contains tens to fifty pages of information. The output is binary information: yes/no. The input/output correlation has a large random and subjective element to it.

As scientists we should only draw conclusions based on the evidence at hand.

If you did not succeed, don't take it personally and give up. Keep applying. Don't write a totally different application next time just because of some speculative reason for past failures.

If you did succeed, don't let it go to your head. Acknowledge the random element in success.

p.s. This is basically the same post I wrote two years ago at the same time. I just thought it was good for me and my colleagues to be reminded of these issues.

Hewson's Kondo narrative

In the reading group this past week we finished the first chapter of Hewson's The Kondo problem to heavy fermions. There is a bit of a narrative which I will try to highlight.

A key aspect is getting to the Kondo Hamiltonian which describes a single magnetic impurity spin interacting with a band of conduction electrons.

Where does this come from?
What is the physical origin of the local magnetic moment?
To understand this one needs to look at the Anderson model Hamiltonian.

Key physics is associated with the Coulomb repulsion U [aka Hubbard] associated with two electrons on the localised orbital associated with the impurity.
First, if one solves the model in the mean-field [Hartree-Fock] approximation one finds that a net magnetic moment can occur, i.e. spin rotational symmetry is broken, for certain parameter regimes. This result was half of Anderson's 1978 Nobel Prize.

Second, one can derive the Kondo Hamiltonian as an effective Hamiltonian for the Anderson model in the limit of large U and small hybridisation [the local moment regime]. This is done via a "canonical" transformation due to Schrieffer and Wolff or via van Vleck's quasi-degenerate perturbation theory. On some level one is "integrating out" the charge fluctuations on the impurity. This is analogous to the way one starts with a Hubbard model and derives a Heisenberg model as the effective Hamiltonian for the spin degrees of freedom in a Mott insulator.
This is done in Section 1.7.

The Anderson model with U=0 [Section 1.4] illustrates some key physics.

a. The existence of virtual bound states within the conduction band. These lead to a resonance and a large peak in the density of states (DOS).

b. The energy scale associated with hybridisation.

c. The Friedel sum rule which connects the phase shift associated with scattering from the impurity with the change in the DOS and the total additional number of states that appear in the conduction band.

 The above three concepts will all be useful for later understanding the Kondo resonance.
It is also pointed out that the non-interaction Anderson model cannot explain the temperature dependence of the spin susceptibility associated with the impurities.

Finally. one introduces the Coqblin-Schrieffer model which is the generalisation of the SU(2) spin symmetry of the spin-1/2 Kondo Hamiltonian to SU(N) symmetry. There are two important reasons for this generalisation.
First, many magnetic impurities involve d and f electrons which have significant orbital degeneracy. For example, Ce3+ has a single electron in the 4f1 configuration which involves (with spin-orbital coupling) total angular momentum j=5/2 and so N=6.
Second, one can consider the large N limit, which turns out to analytically tractable. The corresponding mean-field (slave boson) theory captures a lot of the essential physics [chapters 7 and 8].

Should postdocs teach?

Sometimes postdocs are given the opportunity to teach part [or all] of an undergraduate or graduate course, even though this is not part of their job description.
At UQ there is a formal university wide program ResTeach which aims to get research staff [including senior faculty such as myself] involved in teaching.

If you are a postdoc, should you do it?
Should faculty who pay the salaries of postdocs from their grants encourage or discourage this?

Here are some of the significant advantages to a postdoc of doing some teaching:

• Having the experience listed on your CV may help you get a faculty position at some institutions. For example, in Australia this seems to be almost a pre-requisite these days. Furthermore, if you can be innovative, get high student evaluations, and/or boost enrolments that may be viewed very favourably.
• You usually learn a lot of science from teaching, even lower level courses.
• It can be enjoyable and satisfying.
• If you are fortunate enough to eventually get a faculty position this experience will make it easier handling the formidable challenges of starting out teaching.
• If you are a senior post-doc/research fellow who can supervise undergrads and/or Ph.D students this may help to recruit research students.
• It may create some goodwill towards you in your department. You may be seen as a team player and good departmental citizen.

However, there can be significant disadvantages:

• Foremost, it can consume a large amount of time and energy that reduces your research productivity. Teaching a course for the first time is usually a full-time occupation. You may lose research momentum and that competitive edge you need to land a faculty position or the next research fellowship.
• It may not add a lot to your CV, particularly if your student evaluations are average. They will probably be average or even below average since you are starting out.
• If you don't do a stellar job and/or there are a few disgruntled students your reputation in the department may suffer, perhaps unjustly.

On balance, I think it really depends on the individual: their career goals and career stage. In some cases, I encourage people to do this. In other cases, I discourage it. The main thing is to make a well informed decision which takes into account both the pro's and con's. Postdocs and Research Fellows also need to be wary of the vested interests who will push them in either direction, possibly against the best long-term interests of the postdoc.

I welcome comment, particularly on the situation in other countries.

I get the impression that for major US research universities teaching experience counts for little in landing a faculty position. 

I suspect that for 4-year colleges they expect not just experience but evidence of innovation and positive student evaluations.

Does the doped Hubbard model superconduct?

Answer this question is difficult and controversial.
There is a nice review Numerical studies of the 2D Hubbard model by Doug Scalapino which considers the question.
He claims that in the end the answer is yes.

However, there are several subtleties along the way. I just mention two that I learnt.
To attempt to answer the question one calculates the d-wave pairing susceptibility on a finite lattice.

In determinantal Monte Carlo [which acts in imaginary time and does have an increasing sign problem with decreasing temperature] one observes that as the temperature (=1/beta) decreases the pairing susceptibility increases. This is encouraging. Except, ...

Puzzle/caution/subtlety I
the pairing susceptibility is less than for U=0! 

Clearly there is no superconductivity for U=0 and a key claim of the Anderson paradigm is that large U and correlations are the key for high-Tc. So what is going on?
Scalapino and his collaborators argue that this decrease with increasing U is because U reduces the single particle spectral weight [i.e. the effective mass of quasi-particles increases with increasing U] and so P_d should be compared to the function below which is the value of P_d in the absence of interactions between the holes.

Indeed, one finds that this quantity is less than the calculated P_d, confirming the existence of an attractive d-wave pairing interaction.

Puzzle/caution/subtlety II
finite size effects and dependence on cluster geometry

It turns out that the results don't just depend on the size of the cluster but also its geometry. "One needs to take into account the 4-site local plaquette structure of the order parameter." Z_d is the number of independent near-neighbour plaquettes on a cluster. For the square 16 site cluster (16B) in the figure below Z_d=2. In contrast, for the diamond 16 site cluster (16A) on has Z_d=3. As a result the pairing correlations are suppressed in 16A relative to 16B.

Getting or not getting superconductivity in quantum Monte simulations is certainly subtle. A different technique [constrained path Monte Carlo and which is at zero temperature] used by a different group did not produce long range correlations. [See this PRB from 1999]. I am not sure if this discrepancy has ever been explained to the satisfaction of all parties...

The Nozieres exhaustion problem

The trivial problem is that I find reading the papers of Nozieres difficult and exhausting. They are big on hand waving and physical insight. An earlier post considered his classic paper on a Fermi liquid treatment of the Kondo problem.

Now the real problem.
Today I giving a cake meeting talk about a short 2005 paper Kondo lattices and the Mott Metal-Insulator which Nozieres published in a JPSJ volume "Kondo effect- 40 years after the discovery". It also has several other nice (short) review articles. This paper reviews the resolution of the "exhaustion problem" for Kondo lattices, first raised by Nozieres in a 1998 paper.

In the Kondo effect a single magnetic impurity forms a spin singlet with a collection of metallic electrons within an energy range T_K (the Kondo temperature) of the Fermi energy, E_F. Typically, T_K is much smaller than E_F.

Now consider the Kondo lattice where there are magnetic "impurities" (i.e. localised spins) placed on a lattice of N_L sites. The metal contains of order N_L electrons. How many electrons can form Kondo spin singlets with (i.e. screen) the localised electrons?

N_eff ~ DOS(E_F)*T_K ~ N_L/E_F * T_K  is much less than N_L

Hence, just a few itinerant electrons must screen (form singlets with) many localised spins.
Why is this a problem?
Because in heavy fermion materials (which are described by a Kondo lattice model) one does observe a Fermi liquid ground state, which is a spin singlet with all the localised spins "screened", below some coherence temperature T_coh
Nozieres has a simple argument [which I don't follow and it turns out to be wrong] that
T_coh ~ N_eff/N_L * T_K ~ T_K^2/E_F is much less than T_K

This prediction that T_coh can be much less than T_K and that their ratio has a non-perturbative dependence on the Kondo coupling turns out to be incorrect. This was shown in 2000 with a slave boson theory by Burdin, Georges, and Grempel and confirmed with DMFT by Costi and Manini. There is a nice review of the problem by Burdin.
Nozieres says there is an "obscure puzzle" here: "a phase transition that generates an energy scale much bigger than its transition temperature". He refers to the fact that in the Kondo lattice problem the hybridisation energy Delta [which mixes the localised spin states with the conduction band] is much larger than T_K [its value in the single impurity problem].

Another puzzle for me is how all this relates to a 2008 Nature paper
Scaling the Kondo lattice
by Yang, Fisk, Lee, Thompson, and Pines
which gives an exhaustive (!) analysis of a wide range of experimental data on heavy fermions and only invokes a single temperature scale T* which is much larger than T_K.

What does all this have to do with the Mott transition and the DMFT treatment of it?
The latter can be viewed as a "Kondo lattice problem". At half filling each site contains a "localised" electron which hybridizes and (in the metallic state) forms Kondo singlets with all the remaining electrons.
Nozieres then makes an obscure argument that leads him to the "physical insight" that "the narrow resonance behaviour [present in the metallic phase] is a direct consequence of the residual entropy [of the Mott insulator]"