Hiding the truth

In their wonderful (and provocative) PNAS article, The Theory of Everything, Laughlin and Pines introduced the term protectorate to describe the insensitivity of higher level laws (organising principles) to the details of lower level laws. For example, the laws of thermodynamics are the same regardless of whether the microscopic dynamics of the constituent particles is quantum or classical. Universality in the theory of continuous phase transitions is another important example. Near the liquid-vapour critical point the critical exponents are independent of the chemical composition of the system or of the interatomic forces involved.

Conference highlights

Here are a few things I learnt this week:

Dirk Manske showed that it is very difficult to use electron-phonon coupling to simultaneously explain more than one set of experimental results in the cuprates. Those, such as Devereux and Shen (Stanford) who claim they can must use values for the coupling constants which are as much as an order of magnitude different from what electronic structure calculations give (a case of where the details matter). A nice (but perhaps understated) summary of the results is here.

Jurgen Haase showed how NMR experiments on the cuprates exhibit very large line widths which can be explained in terms of a large spatially inhomogeneous distribution of dopings. Here is one reference, but I would like to find others.
He did not discuss it but he is also a proponent (with Slichter and Williams) of the two-component model for the cuprates, supporting Baryzkin and Pines.

more to follow...

Correlated talks

Yesterday, my colleague Ben Powell gave a talk in the same session as me at the conference. Ben talked about the really nice work he did with Anthony Jacko and John Fjaerestad on the Kadowaki-Woods ratio for strongly correlated electron metals (see here).

A quantity of relevance to their work is the frequency dependence of the self energy, and how it decreases with increasing frequency. It was only listening to Ben's talk, that I realised I showed this quantity in my talk!


For a momentum independent self energy one can calculate the frequency-dependent conductivity, neglecting vertex corrections. Then the left (right) panel gives the frequency dependent scattering rate (effective mass), which is the imaginary (real) part of the self energy.
The top panels are a theoretical calculation and the bottom panels experimental results.

Ubiquitious spin and correlation physics

Today I am giving a talk at the conference. Here is the latest version of the talk. Although it is mostly based on this PRL, I hope I can bring out some of the common physics and issues with a much broader range of systems. A few take home points

• universality (details such as crystal and chemical structures often don't matter)
• some similar physics in organic charge transfer salts and transition metal oxides and heavy fermion compounds
• Kondo physics is even relevant in systems without magnetic impurities!
• Dynamical mean-field captures the crossover from a Fermi liquid (and existence of quasi-particles) to a bad metal at high temperatures.
• But, "low" and "high" are relative (high temperature could be above 20 K!)
• Optical conductivity is a powerful probe to see the destruction of quasi-particles and effects of strong correlations
  

A new iron age (of superconductivity)

Yesterday, Ilya Eremin (MPI, Dresden) gave a really nice talk on the new Ferropnictide superconductors. It was a model of clarity. Here are a few brief notes with a few comments of mine interspersed in parentheses.

Bednorz and Muller changed the landscape of condensed matter physics!
[RHM: Strongly correlated electron materials moved from the peripheral to the centre of the field. ]

Current highest Tc=55 K SmFeAsO1-xFx

Surprising this is a superconductor since it contains iron has a large Hund's rule coupling

Pnictides vs. cuprates: similarities and differences

Similarities
Both are layered (CuO2 vs. FeAs), have d-electrons in a key role, and have AF and SC in close proximity in phase diagram

Differences
FeAs is always metallic, i.e., no Mott insulator in phase diagram
In pnictides d-bands are far from half filling, i.e., almost full (fermi surface close to gamma point) or empty (compensated metal)
EVEN number of electrons (close to 3d6) per iron atom in parent material vs.
one electron per copper atom in cuprate parent

(J. Zhao et al., Nature Materials 2008)

Claims
interactions are smaller than the bandwidth
interesting physis is due to proximity to perfect nesting
whole band is nested, not just the Fermi surface

[RHM: is a key signature of cuprate vs. pnictide difference the size of the magnetic moment in the SDW phase? it turns out to me more subtle than this see below]

For perfect nesting SDW instability occurs for small U

Nesting leads to two competing logarithmic diverges: both in SDW and SC channel
(T.M. Rice for Cr, ) so they must be considered on equal footing and worry about interference effects [this is quite different to the cuprates, where one tends to think in terms of a doped Mott insulator]

[RHM: Similar issues concerning the interference between the particle-hole and particle-particle channels occur in one dimension: cf., Solyom, 1980]

"Toy model":
[I prefer the term "minimal model", perhaps for marketing reasons?]

This has two parabolic bands (alpha and beta band) with identical dispersion and circular Fermi surfaces. One is centred at Gamma point and the other at the corner of the Brillouin zone.
4 types of interactions: both intra-band and inter-band.
There are then 4 possible instabilities:
SDW,
CDW,
s-wave superconductivity
s-wave superconductivity (pi phase shift between bands)

Derives RG equations for the four interactions u1, u2, u3, and u4
[PRB, 2008, Chubukov, Efremov, Eremin]

Strongest instability is SDW then CDW, then extended s-wave. The growth rate of the latter coupling constant changes sign with increasing rescaling (i.e., RG flow) resulting from the interfering logarithms.

Similar results are obtained from functional RG [Visawanath et al, PRL 09]

Can we understand real space magnetism in terms of an itinerant SDW picture?
Two inequivalent As positions leads to ambiguity in Fe sublattice order
Experiment shows (0,pi) order with respect to Fe lattice (stripe like AFM structure)

An alternative picture is that of localised spins in frustrated J1-J2 model. [Uhrig, Holt, Hamer, Oitmaa, and Singh, PRB 2009]. Then the reduced magnetic moment comes from proximity to a quantum phase transition rather than itinerancy.

Look at Fermi surface in unfolded Brillouin zone
Now four pockets alone BZ boundary (i.e., one hole and two electron pockets)
mean-field equations do not specify relative size and magnitude of two
pocket order parameter amplitudes
ground state degeneracy is larger than in J1-J2 model
O(6) degeneracy = 5 goldstone modes

But electron pockets are elliptic, no need for quantum fluctuations in itinerant picture
charge fluctuations are crucial,

Questions:
seems cant get the SDW to SC transition with doping, i.e., moving away from perfect nesting does dominant interaction changes

not clear answer, seems may end up with nodes on fermi surface.

Experimental investigations of Quantum dynamics of excited states of biomolecular chromophores

Last week in Germany I was pleased to meet Roland Wester who does beautiful experiments using crossed molecular beams to image complex chemical reaction dynamics. An example, is a recent Science paper where Roland's group studied a classic S2N subsitution reaction:
Cl^– + CH₃I -> I^– + CH₃Cl

Such experiments can provide significant tests on our basic understanding of reaction mechanisms, quantum dynamics and ab-initio electronic structure calculations.

I was delighted Roland told me he is planning to do some experiments on biological chromophore molecues including the Green Flourescent Protein chromophore. I am interested to learn more about this, particularly how it could provide a test of theoretical work of Seth Olsen and I, such as our recent paper in J. Chem. Phys., concerning photo-isomerisation of the GFP chromophore.

The cast of characters

Hermann Grabert kindly sent the photo of the participants at the 2nd Black Forest Focus on Soft Matter: Quantum efficiency from Biology to Materials Science.

There seems to be uncertainty about anyones position but I guess the camera made a projective measurement of everyones position onto a position eigenstate...

Simulating quantum dynamics in biomolecular excited states

At the Quantum Efficiency workshop in the BlackForest Gerhard Stock (who has just moved from Frankfurt back to Freiburg) gave an excellent talk, Quantum signatures in biomolecular processes. Here are some of my notes.

Strategies to describe complex systems.

Biomolecular dynamics: water through the membrane protein can be modelled well with state-of-the art molecular dynamics simulations.

In such simulations how does one deal with the fact that many bonds are stiff enough that they are only in the vibrational ground state at room temperature? Approximate stiff bonds as fixed.

Rhodopsin: the primary event in vision
Vibrationally coherent photochemistry (lastest experiments by Prokhorenko and Miller, Science 2006) investigated the photo-isomerisation reaction retinal.

Minimal model [Hahn and Stock, JPC B 2000].
A two state model with two vibrational models
Co-ordinate dependent non-adiabatic couplings lead to conical intersection. One can solve the quantum dynamics exactly. Successful simulation of pump-probe experiments up to psec.

Origin of coherent oscillations? Beating between vibronic levels.

Time-dependent wave packet dynamics.
Completely delocalised dynamics on the ground state S0 PES.
Is this quantum or classical? Could be either.

Chaotic vs. regular dynamics.

What features determine the reaction speed and quantum yield?
Interact system with a bath using Redfield theory.
Two alternative couplings to bath.
Conical intersection is crucial.
Mechanism of photochemical funnel CPL 2003.
Environment is important for irreversible transport through the conical intersection.
Subtle interplay of coherence and dissipative localisation.

Vibrational Energy flow in biomolecules
Motivated by Hamm's experiments.
PRL 2009.
Trialanine is the model molecule.

Resonant energy transfer (RET) can describe energy transfer between
neigbouring amide groups. Semi-classical works well for RET because energy levels are close
but not for energy relaxation.

For bilinear coupling, quantum and classical are only different in the populations of levels associated with states.

Correlated conference questions?

That almost aliterates.

After the Black Forest meeting on Quantum Efficiency I flew straight to Sydney for another conference, without even returning home to Brisbane. I landed at 7am and walked in just as the conference welcome from the local Dean of Science was ending. I don't normally do crazy things like this. I am at University of NSW (where I worked from 1994-2000) for the Gordon Godfrey Workshop on Spins and Strong Correlations. Alex Hamilton and Oleg Sushkov are to be commended for the great list of overseas speakers they have attracted. Hopefully I will write something about some of the talks. I managed to stay awake (more or less) until afternoon tea but then had to leave...

Some of the questions I think we need to keep asking for the diverse array of solid materials under study include:

• What properties of a class of materials are universal?
• What are the broken symmetries (and order parameters) associated with the different ordered phases?
• What are the experimental signatures of strong electronic correlations? or, What properties cannot be explained even qualitatively by mean-field theory.
  
• Is the quality/purity of the samples high enough we can be confident that experimentalists are measuring what they claim on what they claim?
• What is the minimal quantum many-body Hamiltonian that can describe a class of materials? How many bands are necessary?
• Is there an variational wave function that captures the essential physics of the competition between the different ground states?
• Is the reliability of a theoretical approximation or numerical method high enough that we can be confident that theorists are calculating what they claim on the model they are studying?
  
• What are the outstanding unresolved questions?

New coherent spectroscopies

Shaul Mukamel (UC Irvine) gave the last talk at conference, Coherent nonlinear optical spectroscopy of biological complexes: from nmr to x-rays. It contained several really new and stimulating ideas. A nice overview is in this recent Accounts of Chemical Research paper.

Heterodyne-detected four wave mixing produces a signal S(t1,t2,t3).
There are three time differences between the four pulses t1, t2, and t3.

Experiments will soon be done in UV and X-ray part of the spectrum.

Joke: Translating Othello into Yiddish with great improvement!

Two-dimensional correlation peaks S(omega1,t2,omega3) gives a direct handle on coupling of modes, and on diagonal fluctuations and noise from lineshapes.

Recent experiments on Helical J-aggregrates reveal the pattern of energy flow.

There are TWO alternative and equivalent theoretical descriptions of these experiments. Eigenstate vs. Quasiparticle (oscillator) description of nonlinear response of excitons.

Same effective Hamiltonian for excitons, and several other systems.
H = site energies + hopping +
two-particle interactions (K coupling is a measure of anharmonicity).

Schrodinger picture. Eigenstates.
Third-order measurements probe single and double excitons.
Feynman diagrams and associated rules greatly help visualisation of the essential physics and aid derivation of equations.

Alternative approach: quasi-particles. Write Heisenberg equations of motion.
If they are linear (because there are no interactions) there is no non-linear spectroscopy. Add bath and solve equations of motion. Response function looks very different from the eigenstate picture. How do we relate the two?

Bethe-Saltpeter equation.

Oscillator picture has advantage numerically since it scales with N, whereas the eigenstate picture scales with N^2. The latter also involves massive cancellations of terms which obscures the physics.

For the FMO complex 7 excitons, 21 double exciton states.

New idea for new experiments. 1.
Measure Double quantum coherence. S(t3,omega2,omega1) shows a picture of which single excitons contribute to the two-exciton wavefunction. This is sensitive to electron correlations.
Greg Scholes has done the first experiment. Photon echo technique is not sensitive to these correlations.

Derive Lindblad equation from a modified Redfield equation.
There are features in some of Flemings spectra which are evidence for 3 exciton correlations.

New idea for new experiments. 2.
Non-linear spectroscopy with entangled pairs of photons.
Possibility of selecting between pathways/diagrams. Different scaling with intensity. (seen in Boston experiments). Control entanglement time can be varied with femtosecond resolution.
Provides a new spectroscopic tool which will work at low intensities.

Quantum efficiency in photosynthetic systems

Josef Wachtveil (Frankfurt) gave a nice talk on quantum efficiency in photosynthetic systems. Here are my rough notes.

First a joke.
Quantum biology?
Moles tunnel into the classically forbidden region. But they make holes everywhere. They are delocalised!
[John Briggs asked if there was an entanglement measure of entropy per mole!].

Arrangement of electron carriers has a common structural motif in many proteins.

Optimisation principle. Change pigment and reduce quantum efficiency.

Electronic coupling between molecules is sensitive to orientation and relative direction of two molecules. Is it optimised?

There appears to be no functional role of the observed vibrational coherence associated with electron transfer.

Non-photochemical quenching (NPQ) in green plants. How does plant deal with excess photon flux? Triplet chlorophyl excitations can produce highly reactive singlet oxygen. Xanthophylll cycle induced by high light or change in pH.

"gear-shift" model as a mechanism for NPQ. Increase no. of conjugated bonds lowers excited state energy can act as an energy dump.

Quantum chemistry (DFT) calculations suggested that charge transfer is a potential quenching mechanism. Fleming group (Science 2005) tested this. Peak is at 1000 nm.

Artificial systems
Beyond vibrationally induced electron transfer in Gratzel cells and CdSe quantum dots coupled with methyl viogen. (Multi-excitons can be produced by a single photons).
Claims to see ballistic wave packet motion in CdSe nanocrystal and it is at 200 cm-1 which is LO phonon frequency.

What is unique about photosynthetic chromophores?

How are the chromophores in photosynthetic proteins different from in other biomolecules? Why does one see quantum coherence in these systems?

They are much more weakly coupled to their environment than other chromophores. Graham Fleming pointed out that their Stokes shift [which is a measure of the reorganisation energy] is orders of magnitude smaller than other chromophores.
Is this because they are membrane proteins and so are more isolated from the decohering effects of the bulk water outside the membrane?

Future challenges in quantum efficiency

Uzi Landman led an interesting discussion this evening. He is very amusing. Here are a few random notes.

"People believe anything if you use words like nano and quantum."
Dean Koontz, Relentness

"The scientist is not the person who gives the right answers but asks the right questions." Claude Levi-Stauss (1908- )

Photosynthesis cycles involves water splitting.
Manganese oxide cube only determined in 2005. Debatable whether this structure can actually be determined with x-ray crystallography.
Where is the water? How many waters? Why is a cube? The cube is a common structural motif. Does symmetry breaking play a role?
For more on this see an earlier post which gives a few of my thoughts on some of the open questions.

Reaction Centre has to absorb 4 photons to establish a large enough potential to do the oxidation.
This system is extremely specific; not a spherical cow.

Why manganese? (Proc. Roy. Soc. paper a few years ago.)

Measure higher order correlation functions on single molecules to determine whether there are truly non-trivial quantum effects.

Major challenge is to assemble in the lab something that self regulates/repairs.

Packing density in light harvesters are optimised to match the photon flux with the turnover rate of biochemical reactions. Components need to be close but not too close.

Bacteriochlorophyls in LH1 and LH2 exhibit super-radiance consistent with a delocalisation of excitons over 2-4 chromophores.

Does redundancy matter?

Theorists should pay more attention to common structural motifs.

Elliot Montroll argued Photosynthetic system should be two-dimensional.
(PNAS in 1974) This was based on arguments involving probability of return to origin for random walks.

It would be good if someone wrote a "Resource paper" on this subject.

The whole question of charge transport in DNA got off to a bad start because of dubious experimental results. Views ranged from superconductor to insulator.
It turns out to be interesting because the diffusion of counterions in the solvent is what dominates the transport.

To what extent does a system need a blueprint to self-assemble?

Plants are not quantum information processors!

First, I correct something I said in my previous post. Contrary to what I said, delocalised one exciton states can be entangled. For example consider 2 chromophores and one exciton
delocalised between them
|psi> = |01>+|10>
where |01> denotes the first chromophore in its ground state and the second chromophore in its excited state. This state actually has maximum entanglement. Hence, a Bell type experiment could establish entanglement between chromophores. However, is this entanglement relevant for functionality in photosynthesis, as claimed by Fleming's group? Specifically, in their Nature paper they speculate that the protein may perform a quantum computation analogous to Grovers algorithm to find the most effecient way to channel the exciton.

Nein! Here is a simple physical argument. Quantum information processing achieves exponential speed up by making use of the complete Hilbert space.
If we have N chromophores, the size of the complete exciton Hilbert space is 2^N. The one exciton sector is a small part of the whole Hilbert space. For example, for the 7 chromophores in the FMO complex it comprises 7/1024 (i.e., less than 1 per cent) of the whole Hilbert space.
If the plant did a quantum computation to decide how to channel the exciton from chromophore A to B it would have to be exploring multiple exciton states. But such states have energies which are comparable to optical photon frequencies and thus orders of magnitude larger than the energy scales associated with fluctuations in the environment and the interactions between the chromophores.

These delocalised exciton states are completely analogous to the Bloch one electron states which occur in crystals (such as silicon). But I don't think quantum information is relevant to understanding solid state physics and devices.

How quantum is biology?

There was a really good discussion at the conference which clarified a few things for me.

Just how quantum are the effects (interference of excitons) that have been observed?
John Briggs asked how this was different from coupled harmonic oscillators?
Where does h-bar enter?
Shaul Mukamel pointed out that as long as one is looking in the one exciton sector the Heisenberg equations of motion just look like classical harmonic oscillators. hbar only enters as omega=frequency=E/hbar.

This is just like how the Bloch equations can be viewed as equations for a damped harmonic oscillator.
These questions about true quantum effects are reminiscent of the birth of quantum optics. People thought photons were necessary to explain spectroscopy. But actually this could all be explained in a semi-classical framework. It was only with experiments such as photon anti-bunching and squeezing that the truely quantum nature of light was established.

To see true quantum effects such as entanglement one will need to look in the two-exciton sector. Then a definitive signature of entanglement would be violation of Bell inequalities. Until such an experiment has been performed I see no justification for making claims that entanglement does exist in photosynthetic light harvesting systems.

Extra-ordinary claims require extra-ordinary evidence.

Quantum principles for functional electronic materials?

Here is the current version of the talk I will give this afternoon at the workshop in Germany on
Quantum efficiency: from biology to materials science.

I am really excited about this workshop since it involves people and topics that so strongly overlap with my interests.

I decided to talk less about the specifics of some of my own research and more about some of the general issues in the field and specifically how the spin-boson model gives us insight into the rates at which transitions occur between specific quantum states in complex molecular systems.

One thing I am still not clear on (convinced of) is:
does quantum coherence necessarily enhance the rate at which processes occur?

Simulation and visualisation of quantum dynamics

ack, a student in PHYS3170 brought to the class attention the site for the WAVEPACKET simulation project. It has some really nice animations of quantum dynamics on potential energy surfaces and non-adiabatic dynamics near a conical intersection.

Quantum coherence in photosynthesis?

In the latest PNAS Peter Wolynes has a nice Commentary, Some quantum weirdness in physiology on a paper by Ishizaki and Fleming, Theoretical examination of quantum coherence in a photosynthetic system at physiological temperature.

Wolynes rightly cautions about invoking quantum effects to explain biological functions but seems convinced by work from Flemings group.

Here, I just explain what I believe is the essential physics in the theoretical paper since it can lost in all the detail. The key time (energy) scales in the calculation are:

• relaxation time of the environment (50 fsec)
• period of coherent oscillations (150 fsec)
• reorganisation energy of the environment , E_R (35 cm-1 ~ 1 psec)
• thermal energy, kB T (200 cm-1 ~ 150 fsec)

A relatively simple calculation using an independent boson model (see for example this paper) shows that there is initially a Gaussian decay of quantum coherence on the time scale, tau_g


Using the estimate E_R ~ 35 cm-1 gives a time scale of about 300 fsec for the decoherence time comparable to that in the detailed simulations of Ishizaki and Fleming. Decreasing the temperature by a factor of 4 will result in a two-fold increase in the decoherence time.

It should also be stressed that this reorganisation energy is an order of magnitude smaller than that estimated for other chromophores in proteins (see Table 2 in this paper). This will only be possible if the chromophore is well isolated from water in the environment.

Subtle structures in a photoactive protein

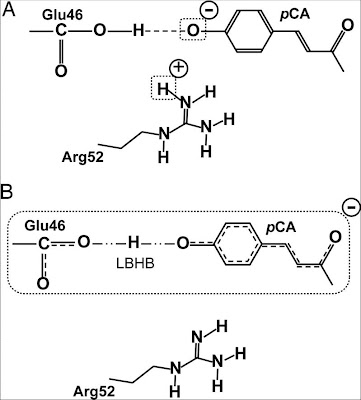
When visiting Irene Burghardt she told me about an important development in our understanding of the chromophore in the Photoactive Yellow Protein (PYP). A recent neutron scattering study [which I wrote a previous blog post about from a different angle] showed that the standard picture (A above) of the charge distribution around the chromophore was incorrect.

It was previously assumed/claimed that the Arg52 and Glu42 amino acids in the protein were protonated and the chromophore was negatively charged. However, the neutron scattering experiment showed that the structures were actually those shown in B above. In particular there is a low barrier hydrogen bond (LBHB) between the Glu42 and the chromophore.

This was also confirmed in an independent NMR study, also recently published in PNAS.

A new class of chemical bonds II

Yesterday in Paris I had some really nice discussions with Philippe Hiberty about valence bond theory. Philippe helped me understand better his work on charge-shift bonding, described in this recent Nature Chemistry paper.

Some signatures of charge-shift bonding are illustrated in the figure above (left click to see a legible version) include:

there is a smaller charge density in between the bonded atoms and there are large fluctuations in this density

the laplacian of the electron density has the opposite sign to that for covalent bonds (compare the C-C bond and the F-F bond).

I also came across this paper by Barbosa and Barcelos. They discuss bonding in halogen molecules in terms of GVB wave functions and suggest that among halogen molecules charge-shift bonding is only responsible for bonding in F2 (flourine). [Note that at the Hartree-Fock level the F-F molecule does not even bond, i.e., there is a meta-stable minimun in the ground state energy vs. internuclear separation, but the binding energy is negative.

I would really like to understand this qualitative difference between the different types of bonding in terms of a simple model Hamiltonian (a two site Hubbard model?) with just a few orthogonal orbitals. Could it just be that the key difference between covalent and charge shift is just the sign of the "hopping integral" between the two relevant orbitals? This will make the anti-symmetric orbital, L - R, more stable than the symmetric orbital, L+R. [L and R denote the frontier orbitals on the left and right atoms respectively].
i.e., the ordering of the sigma and sigma* orbitals below will be reversed.

The anti-symmetric orbital will have the desired properties of a negative laplacian and more density away from the region between the bonds.

Learning to write

It cannot be emphasized enough that learning to write clearly is an incredibly important skill, discipline, and gift that is necessary for survival and success in science.

Can everyone learn to write?

How do mentors/supervisors teach students to write?

These questions are wrestled with in two stimulating posts (and many thoughtful comments) by the Female Science Professor,

literally doomed and escaping from the garden of meaning

I thank Ben Powell for bringing these to my attention.

Seminar at Ecole Polytechnique

Today I had a really nice visit to the condensed matter theory group at Ecole Polytechnique. Here is a copy of the seminar that I gave, Destruction of quasi-particles near the Mott-Hubbard metal-insulator transition. It is largely based on this paper. It was great to give this talk to so many experts on Dynamical Mean-Field Theory.

Talk at ENS

Here is the talk I am giving this afternoon in Chimie at Ecole Normale Superiere on the role of quantum effects on hydrogen transfer reactions that are catalysed by enzymes.
The latest version of the corresponding paper is here.

What is the third state?

A very important question in French history was: Qu'est-ce que le tiers état?

Yesterday I had some really nice discussions with Irene Burghardt in Paris. We have many common interests concerning quantum dynamics of excited states in condensed phases.

In many chemical processes we are interested in understanding the mechanism whereby one gets from state A to B. This is usually via a transition state C which is often believed to be something like a linear interpolation between A and B. However, it turns out that there are important processes whereby a third state is crucial for understanding the quantum dynamics of getting from A to B.

One example that Seth Olsen and I have worked on is Photoisomerisation of flourescent protein chromophores and methine dyes. This preprint, describes in detail the topology of possible potential energy surfaces for a three state model.

Another example that Irene and her collaborators have been working on is relevant to bulk heterojunction organic solar cells. She gave me a copy of this nice review of their work.

The key process is photoinduced charge transfer from a donor molecule D to an acceptor molecule A:

D A + photon -> D* A -> D+ A-

Electronic structure calculations have shown that at a TFB:F8BT polymer heterojunction there is a higher lying charge transfer state (IS for intermediate state) which couples strongly to the exciton state (XT) which is predominantly TFB*.
XT eventually decays to a charge transfer state CT (the "exciplex") which is predominantly TFB+:F8BT-.

Here are the potential energy surfaces they have constructed. Note that the conical intersection between the CT and XT states is at a much higher energy than the Franck-Condon point. The figure is from a recent PRL.

There is some experimental evidence supporting this claim of the role of a third state.

A few questions I have are:

What is the nature of the IS?
It is a dark state. Is it just, TFB-:F8BT+, whereas CT= TFB+:F8BT-?
Or is this third state a particle-hole state of TFB which has the same parity as the ground state and so is dark.

Can we derive this effective three-state Hamiltonian from a four orbital, four electron model [i.e, just one HOMO and one LUMO on each of TFB and F8BT?
Irene says no, one needs to take into account the delocalised nature of the excited states along the polymer chains.

The easiest person to fool is yourself

Key moderating principles I try to keep in mind as I struggle to understand complex molecular materials

-correlation does not imply causality

-extraordinary claims require extraordinary evidence

-Kauzmann's maxim: people will tend to believe what they want to believe rather than believing what the evidence before them suggests they should believe

-use the method of multiple alternative hypothesis

-be mindful of the dangers of curve fitting

-in systems with many degrees of freedom it is very hard to find control variables, because most variables are not independent of one another

-Feynman's warning: the easiest person to fool is yourself

The way things work

Survival and success in science is hard; especially, getting a permanent
job and obtaining research funding.

The questions that are largely irrelevant and many people spend their
time talking about are:

How do you think the system works?
How do you think the system should work (i.e., justly and efficiently)?

but rather

How does the system actually work?

Here are a few tips I give people that may help answer this question with regard to grant applications.

• look at copies of successful applications
• get connected personally; i.e., meet possible reviewers, panel members, program managers
• talk to former ARC panel members (in Australia), current and former program managers (in the US)
• if your university runs workshops where "veterans" give advice, go!
  
• accept the element of randomness in the process...

Three key ideas for organic photonics and electronics

• Electronic correlations can significantly modify the relative energy of excited electronic states, especially near transition states.
• Due to conical intersections between potential energy surfaces non-adiabatic processes can lead to ultrafast internal conversion (transitions between different electronic states).
• The environment has a significant effect on the rate of transitions between quantum states.

But how will we raise the children?

My wonderful wife and kids gave me the complete season two DVD collection of the TV show, The Big Bang Theory. Tonight we watched this great episode where two physicists dating break up because they disagree about the relative merits of string theory and quantum loop gravity. Here is the relevant clip.

Did Bohr keep thinking critically?

A widely circulated story (especially on the internet!, see here, for example) features an undergraduate student giving "creative" answers to a standard physics exam question about how to use a barometer to find the height of a building. The punch line is:

[The examiners] asked the student if he knew the standard answer to the question. “Of course,” he replied. “But I am fed up with high school and university teachers trying to tell me how to think.”

And the name of the student of this perhaps apocryphal story? Niels Bohr, the Danish physicist who won the Nobel Prize for his contributions to quantum theory.

On reflection, there is great irony here, because later in life, Bohr himself "told people how to think", in ways that I consider significantly impeded a range of endevours.

First, the Copenhagen interpretation of quantum mechanics, seems to have been accepted by physicists largely by the force of Bohr's status and personality, rather than by its scientific merits. This is chronicled by James T. Cushing in, Quantum Mechanics: Historical Contingency and the Copenhagen Hegemony.

Second, this "hegemony" led to a dismissal of Einstein's objections to quantum theory and slowed the development of theory and experiments to test the foundations of quantum physics. John S. Bell was a "rebel" who pursued implications of the Einstein, Podolsky, Rosen paradox alone in the 1960's. His work and Aspect's experiments in the early 1980's eventually led to the whole new field of quantum information and many new interpretations of quantum theory, including decoherence based approaches.

Third, Bohr made many highly speculative statements about the implications of quantum theory to other disciplines (including politics and religion) that were accepted uncritically and used inappropriately by some postmodernists. Mara Beller, has chronicled these excesses in a provocative Physics Today article "The Sokal Hoax: At Whom Are We Laughing?", and a book, Quantum Dialogue: the making of a revolution.

I thank Ben Myers and Kim Fabricus for bringing this anecdote to my attention.

Chemical valence bond theory for physicists

The last couple of years I have been learning more about valence bond theory in chemistry. Something that has really helped was a review article in Reviews of Computational Chemistry and a book by Shason Shaik and Philippe Hiberty.

Although the book is intended for chemists I think that (unlike many quantum chemistry books) it is quite accessible to physicists. I really appreciate the emphasis on concepts, qualitative differences, and chemical intuition.

Next week I will meet Philippe in Paris.

A cool Father's day present

We are celebrating Father's Day today because I was away on the actual day. My family just gave me the coolest present! The DVD collection of the complete Season 2 of The Big Bang Theory, a hilarious sitcom involving physics nerds. [They gave me the Season 1 collection for last Christmas!].
If you have not seen it, to get the flavour of it watch this.

Talk on quantum effects in enzymes

Tomorrow morning at the COPE science weekly meeting I am giving a short talk on The role of quantum effects in enzyme catalysed proton transfer reactions. The current version of the slides is here.

Shrinking those huge .eps files

This is a somewhat boring post, but it may help someone.
I have just wasted a lot of time submitting a paper to the arXiv and kept getting rejected because of the large size of the .eps files for the figures. The advice they gave for solving the problem did not help. The .pdf version of the figures was an order of magnitude smaller and so I found the best thing to do was just to convert the .pdf version to .eps. Since I only have Adobe Reader and am using Windows I downloaded this freeware converter. I realise if I was using Unix I could just use pdf2eps. Any better ideas?

Are you nervous? Its just physics!

One of the things I really liked about Nelson's chapter on Nerve Impulses was the figure below. (Left click to make it larger.)



In the caption he says, "Perhaps the most remarkable experiment described in this book."

Why is this data so important and profound?

I would say that it is another defeat for "vitalism" and victory for both reductionism and emergence.

It is a victory for reductionism because it shows how a specific biological phenomena (nerve impulses) can be essentially reduced to a purely physical effect.
It is a victory for emergence because it shows how the shape and speed of the voltage pulses is universal and independent of many of the biological and biochemical details.

The right panel shows the time dependence of the voltage across the membrane of a "live" axon (a single nerve) cell.
In contrast, in the left panel the contents of the cell (a complex biochemical mix!) have been removed and replaced with just a solution containing the same amount of potassium ions as the "live" cell. [But the cell membrane and its ion channels are intact].

In passing, I mention that this does not mean that consciousness is "just" electrical activity. But that is another story....

Nobel prize predictions

From the previous post you will see I was on the Nobel Foundation site and I just noticed that the Physics and Chemistry prizes are about to be announced. Then I thought, who would I predict (see below) and then did a web search to see if anyone else was making predictions.

This post on physics.about.com and the associated links is worth looking at.

I think some of those predictions are focused to much on more recent research.

Here are a few names that I was surprised were not mentioned.

Alain Aspect: experimental tests of Bell inequalities

Frank Steglich: discovery of heavy fermion superconductors

Jun Kondo: magnetic impurities in metals

Nervous and impulsive

I am really enjoying the last chapter of Nelson's Biological Physics. It discusses pioneering work of Hodgkin and Huxley the 1940's which laid the foundations for our understanding of nerve impulse propagation.

Hodgkin and Huxley received the 1963 Nobel Prize in Physiology of Medicine for this work.
[They shared it with John Eccles from ANU]. The Nobel Foundation has a really nice educational "game" on Nerve Signaling.

Nelson notes,

"Many biophysicists regard this work as one of the most beautiful and fruitful examples of what can happen when we apply the tools and ideas of physics to a biological problem."

Biological question: How can a leaky cable (e.g., a neuron) carry a sharp electrical signal over long distances?

Physical idea: Nonlinearity in the cell membrane's conductance turns the membrane into an excitable mdedium, which can transmit waves by continuously regenerating them.

Again, Nelson has really helpful section headings, including:

12.1.2 The cell membrane can be viewed as an electrical network
12.1.3 Membranes with Ohmic conductance lead to a linear cable equation with no traveling wave solutions

12.2.4 The time course of an action potential suggests the hypothesis of voltage gating
12.2.5 Voltage gating leads to a nonlinear cable equation with traveling wave solutions

12.3.1 Each ion conductance follows a characteristic time course when the membrane potential changes
12.3.2 The patch clamp technique allows the study of a single ion channel behavior

Europe trip

In a week I am heading off to Europe for two weeks. The first week will be visiting Universities in Paris The second week I will visit University of Freiberg in Germany and then attend a workshop, Quantum Efficiency: From Biology to Materials Science, part of a series Black Forest Focus on Soft Matter, organised by the Freiberg Institute for Advanced Studies.
I am looking forward to meeting a number of people whose papers I have read but not met yet personally. These include Irene Burghardt, Silke Biermann, Michael Thorwart, Graham Fleming, Peter Hamm, Gerhard Stock, and Shaul Mukamel.
Hopefully I will be writing about their work and the trip soon.

Emergence: a virtual museum exhibit

I2CAM has just opened a new virtual museum exhibit at the Emergent Universe.
I strongly recommend it both to scientists and non-scientists.

Do protons really tunnel in enzymes?

It is a great feeling when you finish a paper you have been working on for a long time.

I just finished (I hope!) a paper, Quantum transition state theory for proton transfer reactions in enzymes, that I wrote with my former students, Jacques Bothma and Joel Gilmore.
I plan to put it on the arxiv early next week and then submit it to Journal of Chemical Physics.

Comments welcome!

The recent book cover below shows the timeliness of the topic.

Does quantum coherence matter in organic solar cells?

At today's COPE science meeting we are discussing a paper, Coherent Intrachain Energy Migration in a Conjugated Polymer at Room Temperature, published in Science early this year by Collini and Scholes. The paper was chosen by Paul Schwenn.
There is also a longer much more detailed description of the work in J. Phys. Chem. A, which helps understand some of the details, particularly because it has some nice pedagogical figures.
Use is made of two-dimensional spectroscopy, for understanding that I find this Figure very helpful.

A key issue in photosynthesis and organic solar cells is the harvesting of light. One wants to channel excitons to "reaction centres" where charge separation will occur, as rapidly as possible and with the maximum efficiency. EET (electronic energy transfer) or exciton transfer usually occurs between molecules via the Forster mechanism (FRET). Often this is incoherent (and irreversible), i.e., there is no phase coherence between the wavefunction of the excitation on the donor and acceptor molecules. If phase coherence is present one can observed quantum interference effects such as Rabi oscillations associated with an excition oscillating back and forward between the donor and acceptor.

An important question is whether coherent transfer will increase the transfer rate and efficiency. Most people seem to claim it does but this is not clear to me. Some of these issues are discussed in an earlier post on similar experiments on a photosynthetic system.