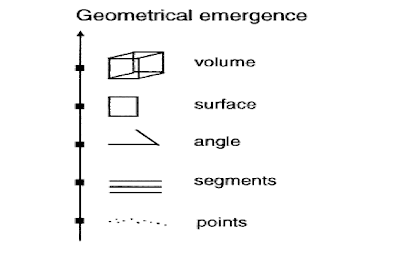
A nice article Emergence in Chemistry by P.L. Luisi uses the figure above to illustrate emergent properties and particular issues they raise. The figure illustrates how there is an increase of complexity as one goes from points to line segments to two-dimensional shapes to three-dimensional objects with volume. Note that the notion of angle has no meaning at the stratum of points and segments, and the notion of volume is not present at the stratum of surfaces or of angles. The first issue this illustrates is that, at each higher stratum there are unique properties and concepts which are not present at the level of the lower strata.
Although emergent properties can sometimes be rationalised a posteriori they are difficult to anticipate or forsee. For example, it is not clear that a cube can be predicted in a flat world where a cube has not been seen before. A cube can be rationalised a posteriori in terms of right angles and of eight segments of equal length. However, a priori these segments can be assembled into many different structures with dimensionality one, two, or three. A cube is just one of many possibilities.
The third issue that emergence in geometry illustrates is: emergent properties at one stratum are associated with a modification of the properties of and the relationships between the constituent components which are from the lower stratum. For example, defining a cube leaves the eight constituent line segments in a very particular relationship and they no longer have open ends.
A fourth feature, not mentioned by Luisi, is that the symmetry of the cube is also an emergent property. We note that it is independent of structural details such as whether the cube is solid, or made of line segments of a particular thickness, or whether the cube represents a specific spatial arrangement of eight atoms. Furthermore, the most insight into cubic symmetry and its consequences is achieved by regarding the cube as a three-dimensional object rather than an assemblage of line segments.




There are some very nice points about this example. But I also think it's important to stress something. Emergent properties are, as you say, very hard to predict. But they are not impossible to predict.
ReplyDeleteYou say that "it is not clear that a cube can be predicted in a flat world where a cube has not been seen before." But, we live in a 3d world (a least so far as low energy processes are concerned). And we have predicted hypercubes and studied geometry in many higher dimensions.
A more important example is Bose-Einstein condensation, which was predicted long before superfluid He was observed.
I would argue that, perhaps, the most important problem in theoretical physics today is to learn how to predict new emergent phenomena. Further, I would argue that, perhaps, the most important problem in experimental physics is to learn how to achieve new emergent phenomena in a controlled way rather than waiting for serendipitous discoveries. I would strongly recommend Fleming and Ratner's discussion [Phys. Today 61, 28 (2008)] of this.
Thanks, Ben. I agree I overstated the case. I hope others will post comments to clarify my thinking.
ReplyDelete"However, a priori these segments can be assembled into many different structures with dimensionality one, two, or three. A cube is just one of many possibilities."
ReplyDeleteSo what criteria are used to select the cube over these other possibilities? Is it just a case of a thing that we like emerging from a crowd of things that we don't like as much?
This relates to the following basic question I have about emergence in CMP.
The same microscopic Hamiltonian gives rise to a large number of qualitatively different macroscopic phases (depending on fine tuning of its parameters). So part of the problem in predicting emergent phenomena is just that there are many candidates, most of which might never occur in accessible nature. But my understanding is that this is not the interesting part of the problem. Rather, that the majority of these possibilities will be dull and the interest is in a small minority of special cases. These are the cases (like superfluidity) that really call for new concepts. (I guess 'dull' is defined as everything that we can understand well enough WITHOUT new concepts.)
Is this a shared view? Or do we just like superfluidity because we observe it and just like cubes because cubes are the kind of thing that we like?
This is a very germane example, and a tantalizing hint of the power of exterior algebras in many-body physics.
ReplyDeleteI think it's a great analogy, but I'm not clear how far to take it comparing it to the complexity that emerges in regular physics.
ReplyDeleteAdding higher dimensions isn't *quite* the same thing as adding more particles, is it? I mean, yes you need more parameters to define your state, but in one case you're changing the laws of physics, while in the other you're uncovering unexpected (typically many-body) phenomena that are based on the same simple (haha) rules, and hence discover another new large scale law/theory/phenomena.
I really like your comment, Ben, about predicting emergent phenomena. Nice!