Dispersion kinks and spin fluctuations

A recent post considered the problem of deconstructing the kinks that occur in energy versus wavevector dispersion relations in some strongly correlated electron systems.

I have now read two of the related references to the recent PRL I discussed. A nice earlier PRL discusses how kinks occur in the temperature dependence of the specific heat. Furthermore, the authors use an obscure formula from the classic AGD to show that these kinks are related to the kinks in the self energy.

Emergent Collective Modes and Kinks in Electronic Dispersions
Carsten Raas, Patrick Grete, and Götz S Uhrig

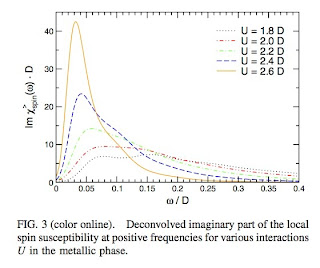
They calculate the self energy and the frequency dependent local spin susceptibility for the Hubbard model at half filling using Dynamical Mean-Field Theory (DMFT). The latter quantity is shown below. As the Mott insulator is approached a low-energy peak develops in the spin susceptibility. This reflects the large spin fluctuations in the metallic phase as the electrons become more localised.

Aside: the slope of this curve at zero frequency is proportional to the NMR relaxation rate 1/T_1.

The frequency/energy of the peak is the same as the frequency of the kink in the self energy and the local Greens function, as shown below.

Note how there is an emergent low-energy scale much less than the energy scales in the Hamiltonian; a profound characteristic feature of strongly correlated systems.

From the correlation shown above the authors "deduce" that the spin fluctuations "cause" the kink. I suspect this has to be true but the logic does not appear completely water tight to me.
Nevertheless, it is a beautiful result.

All this is at zero temperature. I would be very interested to see how the spin susceptibility evolves with increasing temperature, particularly as one goes into the bad metal region.
It would also be interesting to see how this physics persists beyond DMFT.