First, it is amazing that using fancy techniques based on capacitors one can measure changes in lattice constants of less than one part per million!
Second, there is some interesting thermodynamics that follows from the Maxwell relations. The isotropic thermal expansion is related to the variation in the entropy with pressure
Hence, in a Fermi liquid metal the thermal expansion versus temperature should have a linear temperature dependence at low temperatures.
Below, I show the temperature dependence of the thermal expansion (along two different crystal directions) for the heavy fermion compound CeRu2Si2, reported in a PRB article. The lower two curves are from the structural analogue LaRu2Si2 which does not have a contribution from 4f electrons.
The peak in the cerium compound is arguably associated with the formation of a coherent Fermi liquid below a coherence temperature of about 10 Kelvin. Below that temperature the thermal expansion is approximately linear in temperature.
How big is the effect? One way to quantify it is terms of the Gruneisen parameter [see Ashcroft and Mermin, page 493].
where T_i is the characteristic temperature scale of the entropy [here the Kondo or coherence temperature]. For heavy fermion compounds Gamma is two orders of magnitude larger than for elemental metals or the values of order unity, typically associated with phonons in simple crystals. This implies an extremely strong dependence of the characteristic temperature on volume. As far as I am aware there is no adequate theory of these large magnitudes.
There is a recent preprint which reports the temperature dependence of the thermal expansion in the iron pnictide KFe2As2 and relates it to a coherent-incoherent crossover like that discussed above.
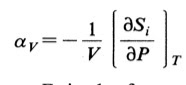




Hello,
ReplyDeleteYour blog posts are very interesting and I enjoy them a lot.
I can leave some comments on this post.
So, Gruneisen ratio, Gamma, is known experimentally/theoretically to diverge as a function of temperature at QCP(PhysRevLett.91.066405,PhysRevLett.91.066404). If a heavy fermion system is close to QCP, Gamma increases strongly with decreasing temperature and saturates with very large value at low temperatures.
There's also a magnetic-field analogue of Gamma, magnetic Gruneisen ratio, Gamma_H. Gamma_H~(dS/dH)/(dS/dT) is expected to diverge at H-induced QCP, if H is driving a QC system away from QCP. (PhysRevLett.102.066401)
Yoshi Tokiwa
Dear Colleagues,
DeleteLet me offer some comments on this post. Measurements of magnetic Gruneisen ratio are of great interest, for these can be used when constructing a general phase diagram of heavy-fermion metals. The scaling behavior of magnetic Gruneisen ratio reveals the nature of QCP. Please see EPL, 106, 37001 (2014); doi: 10.1209/0295-5075/106/37001
With warm regards,
Vasily Shaginyan