omega_c is the cyclotron frequency which is proportional to the magnetic field B and independent of temperature.
tau is the scattering time, which is temperature dependent and field independent, and should have the same temperature dependence as 1/rho where rho(B=0) is the zero field resistivity.
These observations lead to Kohler's rule which is obeyed by simple metals.
A plot of the ratio of the rho(B)/rho(B=0) versus B/rho(B=0) should be independent of temperature. In 1995 Ong's group observed significant violations of Kohler's rule in the underdoped and overdoped cuprates.
In 1998 I pointed out that in one mysterious organic metal there were also significant violations. The paper also has an extensive discussion of reasons why Kohler's rule can fail.
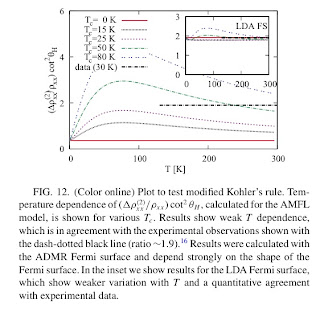
Recently, Jure Kokalj, Nigel Hussey and I wrote a paper which showed that a wide range of transport properties of overdoped cuprates could be quantitatively described by an anisotropic marginal Fermi liquid picture. A referee suggested that we would not be able to describe the temperature dependence of the intra-layer magnetoresistance. It turns out that this also violates Kohler's rule but satisfies a "modified" form where omega_c*tau is related to the Hall angle. We found that with our model we could describe the available experimental data but the magneto-resistance was remarkably sensitive to the details of shape of the Fermi surface. The results are discussed in detail in our paper which just appeared in Physical Review B.
No comments:
Post a Comment