Spin fluctuation dynamics in bad metals

In a Mott insulator the electrons are localised leading to local magnetic moments that weakly interact with one another via superexchange. This means there is a new low-energy scale associated with spin dynamics. But, at the level of Dynamical Mean-Field Theory (DMFT) there is no superexchange and the local frequency-dependent spin susceptibility is a delta function, as discussed here.

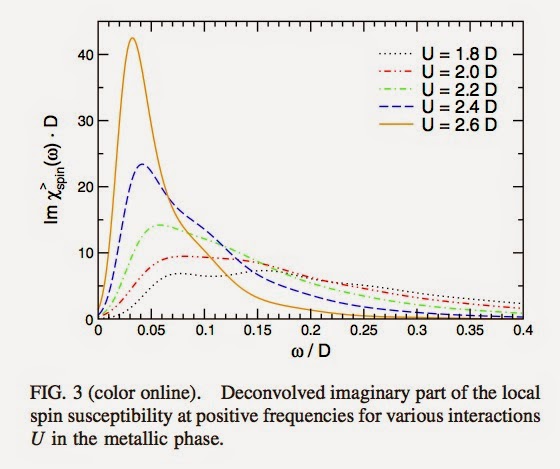
In a Fermi liquid the charge and spin degrees of freedom are both delocalised and the energy scale for spin dynamics Es is defined by the Fermi energy (or coherence temperature). As the Mott insulator is approached Es becomes small, much less than the bare Fermi energy. Furthermore, Es is associated with “kinks” in the quasi-particle dispersion relations seen in Angle Resolved PhotoEmission Spectroscopy (ARPES) experiments on strongly correlated materials. This is discussed in this post which features the graph below for zero temperature.

However, in the bad metal state, it is not clear what the spin fluctuation excitation spectrum is, as it has not been calculated yet. It is not clear to me why, although I know from conversations it is partly due to technical challenges associated with calculating real frequency correlation functions over a wide temperature range. This earlier post discusses the slow spin dynamics in a bad metal when Hund's rule matter.
I am interested in a similar calculation for a single non-degenerate Hubbard model, i.e. how does chi_s(omega) evolve with temperature.

The total spectral weight should be large due to the local magnetic moments associated with the breakdown of Kondo screening associated with the Fermi liquid to bad metal crossover that occurs with increasing temperature.

Understanding and describing the spin dynamics is particularly important, since it will may help distinguish between two alternative pictures of the bad metal,
(i) highly damped quasi-particles or
(ii) almost localised charges with localised spin degrees of freedom,
i.e. is the bad metal closer to a Fermi liquid or a Mott insulator?
In other words, is a wave vector or spatial (waves or particles) picture most appropriate?

Calculations of the specific heat and the uniform static spin susceptibility (using the Finite Temperature Lattice Method) for a Hubbard model on the triangular lattice at half filling, found little change as one went from the bad metal to the Mott insulator. My intuition is that this suggests the bad metal spin dynamics are like those in the Mott insulator, but the only way to clearly show that is through an explicit calculation of chi_s(omega).