Low energy scales near the orbital-selective Mott transition

One of the most fundamental and profound concepts in quantum many-body theory is the emergence of low energy scales that are much smaller than the energy scales in the "bare" Hamiltonian.
For example, in a metallic phase near the Mott transition in a single band system, there is the energy scale associated with a Fermi liquid. Studies using Dynamical Mean-Field Theory (DMFT) have shown how this scale is associated with ``kinks'' in the quasi-particle dispersion relation and is related to the energy scale for spin fluctuations.

The problem of the Mott transition in multi-band systems (degenerate orbitals) is fascinating and of renewed interest since the discovery of iron-based superconductors. A basic question concerns how the Mott transition is qualitatively different from in single band systems. More specifically, how does a Hund's rule coupling change things?

One new concept is that of an orbital-selective Mott transition. This is where one or more of the bands remains metallic but others become Mott insulators. This concept was originally introduced to explain the intriguing properties of Ca_xSr_2-xRuO4 with x ~ 0.5: it is metallic but has localised spin-1/2 magnetic moments.
[For a critical discussion see the  nice review Strong correlations from Hund's coupling by Antoine Georges, Luca de' Medici, and Jernej Mravlje.]

One might expect that near this transition there are separate low energy scales associated with each of the bands and that these scales are quite different for the bands that become insulator.
However, this is not the case.

There is a nice paper
Emergence of a Common Energy Scale Close to the Orbital-Selective Mott Transition 
Markus Greger, Marcus Kollar, and Dieter Vollhardt

They use DMFT to study a two-band Hubbard model with different bandwidths. They calculate the one-electron spectral functions, the electronic self energy, and the dynamical spin susceptibilities.

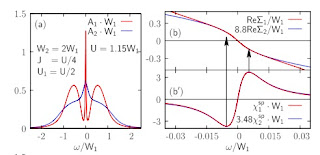
The left panel below shows the spectral functions for the two bands. Note how for one the quasi-particle peak width is much smaller than the other.
The right panel (top) shows the energy dependence of the real part of the self-energy for the two bands. Surprisingly, the kink occurs at the same energy.
Furthermore, the bottom of the right panel shows that this peak corresponds to the peak in the dynamical spin susceptibility for both bands.

The figure below shows that "If the Hund’s rule coupling is sufficiently strong, one common energy scale emerges which characterizes both the location of kinks in the self-energy and extrema of the diagonal spin susceptibilities."

The authors then give a physical explanation of this energy scale from a two-impurity Kondo model.