2 Delta(0)/kTc = 3.5
Most elemental superconductors are consistent with this value. Some such as Hg and Pb have larger values, but these can actually be calculated when strong coupling effects are taken into account, via the Eliashberg equations.
Unconventional superconductors (cuprate, organic, heavy fermion, iron based) have resisted a simple unifying theory and universal trends, comparable to the stellar success of BCS theory. For example, the gap/Tc ratio is all over the place. However, there has been some progress for the iron-based superconductors. Recent ARPES results (summarised in the figure at the bottom below) have shown a universal ratio, of about 7.2 for a wide range of materials.
A fascinating feature of these iron-based materials is the nature of the metallic state that undergoes the superconducting instability. I have written several blog posts about the Hund's metal. One important feature is that there is relatively low coherence temperature below which a Fermi liquid metal forms, and there is a correspondingly low energy scale Omega0 associated with spin fluctuations, which become very slow. This arises from the rich Kondo physics associated with the multi-orbital character of the system. Furthermore, the spin fluctuation spectrum has a power law dependence above Omega0.
The above ideas come together in an interesting preprint
On the Superconductivity of Hund's Metals
Tsung-Han Lee, Andrey Chubukov, Hu Miao, Gabriel Kotliar
They consider a single band superconductor described by the strong-coupling Eliashberg equations where the frequency dependence of the (effective) electron-electron attraction is given by
where the exponent gamma is treated as a variable. The Eliashberg equations are solved (for a single band) and give the following relationship between the gap ratio and the exponent gamma.
The value of gamma=1.2 is that associated with the relevant Kondo problem above the coherence temperature. The gap ratio corresponds to the black dashed line in the graph below.One thing should be stressed here is that one is observing a transition from an incoherent metal into a superconductor, unlike in the BCS situation where the transition is from a coherent Fermi liquid.
I thank Alejandro Mezio for bringing the paper to my attention.
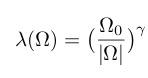






No comments:
Post a Comment