Ising model basics

The Ising model is a paradigm in both statistical mechanics and condensed matter physics. Today for most theorists it is so familiar that some of its historical and conceptual significance is lost.
Previously, I posted about what students can learn from computer simulations of the Ising model.

If you had to talk about the Ising model to an experimental chemist what would you say?
[Last week I had to do this].

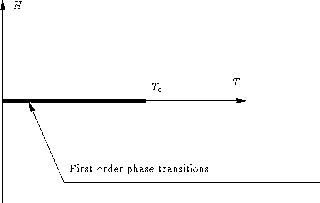
The Ising model is the simplest effective model Hamiltonian that can describe a thermodynamic system that undergoes a first-order phase transition and has a phase diagram containing a critical point.

On each site i of a lattice one defines a spin sigma_i= +1 or -1, representing spin up or spin down.

The Hamiltonian H is

J_ij describes the interaction between spins on sites i and j. In the simplest version the interactions are only between nearest neighbours, and have the same value J.
h is the external magnetic field.

If J is positive, the ground state at h=0 is a ferromagnet.
If J is negative, the ground state at h=0 is an anti-ferromagnet for a bipartite lattice.

[Caution: just like for the Heisenberg model, some authors define the Hamiltonian with the opposite sign of J].

For h=0 there is a critical point at a finite temperature Tc, for lattices of dimension two and higher.

The spins sigma_i= +/- 1 defined at each lattice site i, were originally to represent the atomic magnetic moments in a ferromagnetic material. However, the sigma's can represent any two states of the site i. For example, the ``spin'' or pseudo-spin can represent the presence or absence of an atom or molecule in a ``lattice gas'', atom A or atom B in a binary alloy (mixture), or the low-spin and high-spin states in a spin-crossover material.

The mean-field theory of the Ising model is mathematically equivalent to the thermodynamic theory of binary mixtures with an entropy of an ideal mixture.
There is a nice discussion of such mixtures in Section 5.4 [and the associated problems] of Introduction to Thermal Physics by Schroeder.
[Here are the slides for a lecture I have given based on that text].
Chapter 15 of the text by Dill and Bromberg is also helpful as it has more detail.
Neither text makes an explicit connection to the Ising model. Following this paper on alloys, one has

This is shown in Section 8.1.2 of James Sethna's text, Statistical MechanicsEntropy, Order Parameters and Complexity.

When interactions beyond nearest-neighbours are included in the Ising model or when the lattice is frustrated (e.g. fcc or triangular) a richer phase diagram is possible. Examples include the ANNNI model and some models for spin-state ice considered by Jace Cruddas and Ben Powell.