Tuning the dimensionality of spin-crossover compounds

An important question concerning spin-crossover compounds concerns the origin and the magnitude of the interactions between the individual molecular units.

There is a nice paper
Evolution of cooperativity in the spin transition of an iron(II) complex on a graphite surface
Lalminthang Kipgen, Matthias Bernien, Sascha Ossinger, Fabian Nickel, Andrew J. Britton, Lucas M. Arruda, Holger Naggert, Chen Luo, Christian Lotze, Hanjo Ryll, Florin Radu, Enrico Schierle, Eugen Weschke, Felix Tuczek, and Wolfgang Kuch

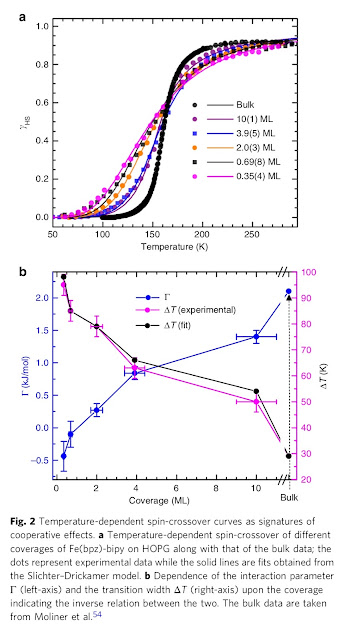
An impressive achievement is the control of the number of monolayers (ML) of SCO molecules deposited on a highly oriented surface pyrolytic graphite. The coverage varies between 0.35 and 10 ML. The shape of the spin-crossover curve changes significantly as the number of monolayers varies, as shown in the upper panel below.

The natural interpretation is that as the number of monolayers increases the interaction between molecules (co-operativity) increases. This can be quantified in terms of the parameter Gamma in the Slichter-Drickamer model [which is equivalent to a mean-field treatment of an Ising model], with Gamma = 4 z J where z=number of nearest-neighbours and J=Ising interaction.
The blue curve in the lower panel shows the variation of Gamma with ML.

The figure above and Table 1 shows that for ML=0.35, Gamma=-0.44 kJ/mol is almost zero for ML=0.7, and then monotonically increases to 2.1 kJ/mol for the bulk.

Does that make sense?

The magnitude of the Gamma values is comparable to those found in other compounds.

The negative value of Gamma for ML=0.35 might be explained as follows. Suppose a monolayer consists of SCO molecules arranged in a square lattice. Then ML=0.33 will consist of chains of SCO molecules that interact in the diagonal direction. If the J_nnn for this next-nearest neighbour interaction is negative then the Gamma value will be negative.

For a monolayer on a square lattice, Gamma= 16 (J_nn + J_nnn). J_nn will be positive and so if it is comparable in magnitude to J_nnn then Gamma will be small for a monolayer.

For a bilayer, Gamma = 16 (J_nn + J_nnn) + 4 J_perp, where J_perp is the interlayer coupling.
For the bulk, Gamma = 16 (J_nn + J_nnn) + 8 J_perp.

This qualitatively explains the trends, but not quantitatively.

The authors also note that the values of Delta E and Delta S obtained from their data vary little with the coverage, as they should since these parameters are single-molecule properties. This also means that the crossover temperature, T_sco also varies little with coverage.

A more rigorous approach is to not use mean-field theory, but rather consider a slab of layers of Ising models. The ratio of the transition temperature T_c to J_nn increases from 2.27 for a single layer to 4.5 as the dimensionality increases from d=2 to d=3.
[In contrast, for mean-field theory the ratio increases from 4 to 6].

If the crossover temperature T_sco is larger than T_c, [as it must be if there is no hysteresis] and assuming J_nn does not change with coverage, then as the coverage increases the crossover temperature becomes closer to the critical temperature and the transition curve will become steeper, reflected in a smaller transition width Delta T (and a correspondingly larger effective Gamma in the Slichter-Drikamer fit). This claim can be understood by looking at the last Figure in this post.