An important question is what is the relationship (if any) between the two methods?
Given that the two methods are formulated in quite different ways it was not clear to me at all whether these question could be answer in any sort of definitive way.
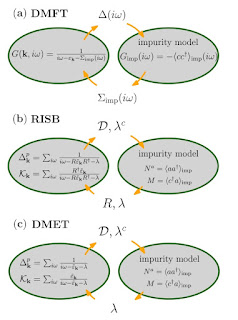
There is a very nice paper which does answers this question in a precise way, with the bonus of also giving the relationship of both methods with rotationally invariant slave bosons (RISB).
Dynamical mean-field theory, density-matrix embedding theory, and rotationallyinvariant slave bosons: A unified perspective
Thomas Ayral, Tsung-Han Lee, and Gabriel Kotliar
The main results are summarised in the Figure below. A result that is useful and insightful is that DMET corresponds to RISB with the quasi-particle weight set to unity (Z=1). There is then no band narrowing associated with the correlations. Given this is a key aspect of strongly correlated electron systems, I think this is a significant shortcoming of DMET. I am also a bit confused about how DMET can then capture a Mott transition.
Hi Ross,
ReplyDeleteTo my understanding, Gabi's paper is a discussion only of the connection to the single-site DMET. It is indeed true that there is no Mott transition in single-site DMET as we discussed in our original paper. However, metal-insulator transitions without AFM order occur in the two-site DMET, and band narrowing also occurs in DMET when you go beyond the single-site formalism.
I think this discussion highlights an important difference in the motivation behind DMET and DMFT. One way to see a theory like DMFT is to view it as offering fundamental information about a problem even in its single site form, in the same way that one obtains understanding from a single site mean-field treatment of the Ising model. The other perspective is that the physics of a single-site effective model is not what one is really interested in; one is interested in the thermodynamic limit, and quantum embedding methods (such as DMET and DMFT) accelerate the convergence to the TDL by incorporating fluctuations across the boundary. DMFT was written down with the first perspective in mind, while we developed DMET with the second perspective in mind. From this second viewpoint, the more important question is not so much how much physics one extracts from the single-site model, but how rapidly one converges to the TDL within the formalism and with computational effort. Our work on DMET is always done with clusters that are (relatively) large - e.g. we have used 32 sites in our recent study of stripes (arxiv:1701.00054) and up to 100 sites at zero Kelvin at half-filling (arxiv:1608.03316). As a computational formalism one then sees benefits to carrying out embedding in the frequency independent DMET formalism when trying to reach the TDL.
Garnet
Garnet,
DeleteThanks for the helpful clarification.