In my previous post about the 2016 Nobel Prize in Physics I stated that the Kosterlitz-Thouless transition was a classical phase transition (involving topological objects = vortices), in contrast to the quantum phase transitions associated with topological phases of matter.
However, on reflection I realised that it should not be overlooked that there is something distinctly quantum about the KT transition. In a two-dimensional superfluid it involves the binding of pairs of vortices and anti-vortices. These each have a quantum of circulation (+/-h/m where h is Planck's constant and m is the particle mass).
At the KT transition temperature Tc there is a finite jump in the superfluid density rho. The value just below Tc is related to Tc by
Note that Planck's constant appears in this equation.
In a classical world (h=0), Tc would be zero and there would be no KT transition!
This universal relation was derived by Nelson and Kosterlitz in 1977
The figure below contains a range of experimental data testing this relation.
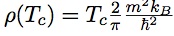





I'm not sure what you mean by "there is something distinctly quantum about the KT transition"... Classical 2D XY spins (i.e. planar arrows in 2D, nothing specifically quantum about them) have a KT transition. And a field theorist would argue that the KT transition of 2D superfluids is also classical, in the sense that only the zero Matsubara frequency part of the field is involved at the (finite temperature) transition.
ReplyDelete(Of course, superfluid are quantum in essence, so the effective classical theory has hbar appearing. But it's not the case for classical arrows.)
Starting from that, I would then argue that the zero-temperature superfluid to Mott insulator transition in the 1D Bose-Hubbard model (which is a KT transition for integer filling) is quantum, in the sense that the vortices are both in space and (imaginary) time.
All of that to say that whether something is classical or quantum depends on the (sub-)field.
I also disagree with the assessment that there is some quantum here. The flux quantum comes in, but this is only an effective charge in the mapping to a Coulomb plasma. So its not any more quantum than a usually classical plasma. Of course the objects in a plasma have charge and you need QM to describe charge. But given a charge, there is nothing else quantum going forward. In the universal jump criterion Planck's constant only appears because people want to put it in the "wrong" units of density. If instead you express the KT transition temperature in units of the microscopic stiffness parameter of the XY spins, then there is no Planck's constant appearing.
ReplyDeleteThanks for the comments. I agree up to a point.
ReplyDeleteBut, I think there is an issue of interpretation here. I am merely pointing out that the "charge" on the vortices is quantised and involves Planck's constant. Similarly the superfluid stiffness involves Planck's constant. I think it is a matter of "taste" as to what the "right" units are. I think you could make the same argument that the degeneracy pressure of a Fermi gas is not quantum because hbar just enters the formula if you use the "wrong " units involving the density.
This reminds me of debates about "is the double slit experiment quantum?" I have heard quantum information types claim it is not because you can see it with classical waves.
So, I stand by my claim that there is quantum dimension to the KT transition in superfluids. But, I acknowledge all of the above objections.
Thanks for engaging in the debate.
As I said, I completely agree that the KT transition for 2D superfluid has a quantum origin, in the sense that one need a single valued (macroscopic) wave-function to define the vortices.
ReplyDeleteWhat I wanted to stress is that the KT transition itself has nothing quantum itself. You can imagine performing an experiment with purely classical object that would still show a KT transition.
This is much the same with topological insultators. The presence of edge-state in a gap between two excitation bands has nothing quantum, and indeed people have created classical systems that have edge states.