Highly dispersive electron relaxation and colossal thermoelectricity in the correlated semiconductor FeSb2
Peijie Sun, Wenhu Xu, Jan M. Tomczak, Gabriel Kotliar, Martin Søndergaard, Bo B. Iversen, and Frank Steglich.
The main results that are a struggle to explain are in the figure below.
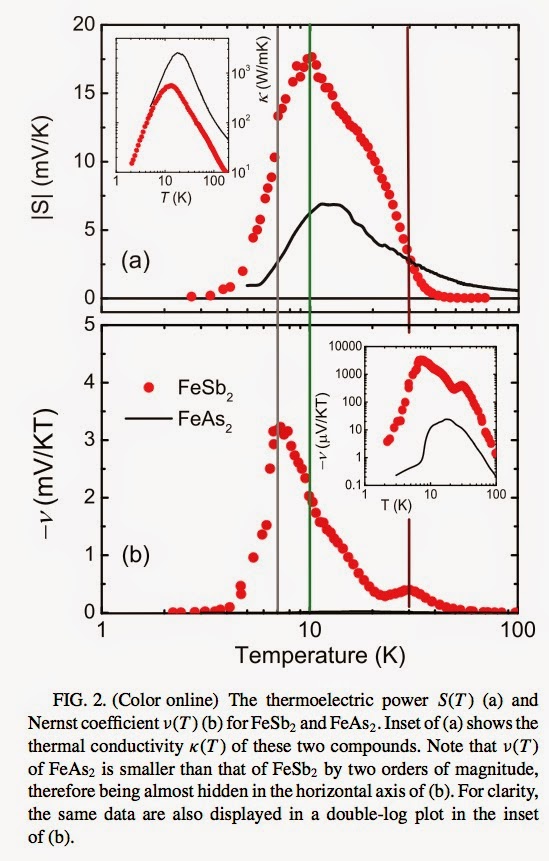
The top panel shows the temperature dependence of the thermopower [Seebeck coefficient] of FeSb2 [red] and the isoelectronic FeAs2.
First, notice the vertical scale is tens of mV/K. In an elemental metal the thermopower is less than a microV/K. In a strongly correlated metal it can be tens of microV/K. [see for example this earlier post].
Why is it so large? Why is the Sb compound so much larger than the As compound?
In a simple model of a band semiconductor S ~ k_B/e * gap/k_B T. But here the Sb compound has the smaller gap.
Also, why is there a maximum in the temperature dependence, S(T) going to zero with decreasing temperature.
In an attempt to elucidate these subtle issues the authors have also measured the Nernst effect and the magnetoresistance. The Nernst signal is also colossal, being of the other of mV/KT for FeSb2, which is two orders of magnitude large than that for FeAs2.
The authors also consider a simple analytical model of a semiconductor with an energy dependent scattering rate to see what properties that can explain: some but not all. A strongly energy dependent scattering rate is also needed; this can occur in the case of Kondo physics, for example.
They also find some interesting relations between Seebeck, Nernst, Hall mobility, magnetoresistance, and the thermal mobility.
It is helpful to read the paper in conduction with an experimental review and this earlier theory paper,
Thermopower of correlated semiconductors: Application to FeAs2 and FeSb2
Jan M. Tomczak, K. Haule, T. Miyake, A. Georges, and G. Kotliar
To further complicate all of the above it seems that the results can be quite sample dependent, and the results varying significantly, even by orders of magnitude between different groups. One clue is that it seems that FeSb2 is very close to a metal-insulator transition, seen in some samples but not others…
Much remains to be done...
Just a few comments.
ReplyDeleteStating that "S(T) going to zero with decreasing temperature" on a mV/K scaling is strange for me. Also S(T) is the entropy per charge carriers so in a clean systems you would not expect S(T~0 K) to be large especially on a mV/K scaling. Anyway, you will rarely see S(T) close to 0K in an insulator as the thermal noise from the large resistance would make any measurements at the micro volts level very hard.
The resistivity of the FeSb2 sample, shown in the paper, doesn't seem to diverge even at 2 K which would indicates a bad metal and not a semiconductor ground state.
Aside from this, I agree that this is interesting. At first, I thought that it was a phonon-drag effect.