How bad metals turn good: spectroscopic signatures of resilient quasiparticles
by Xiaoyu Deng, Jernej Mravlje, Rok Zitko, Michel Ferrero, Gabriel Kotliar, and Antoine Georges
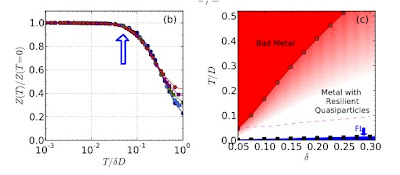
They study a doped Hubbard model using Dynamical Mean-Field Theory (DMFT). Although the ground state is a Fermi liquid this is only a good description at very low temperatures. In particular, the quadratic temperature dependence (characteristic of a Fermi liquid) only occurs below a temperature of about 0.05 delta D [where delta=doping and D=band width]. But, well-defined quasi-particles still exist all the way up to the "bad metal" region at which the mean-free path is comparable to the lattice constant.
The strong correlations lead to a significant particle-hole asymmetry (in the self energy and single-particle density of states) via the subtle interplay of the lower Hubbard band with the quasi-particle peak in the density of states.
To me this all illustrates how much (but obviously not all) of the rich physics seen in strongly correlated materials can be captured by DMFT.
Note added. I am told that the axis label on the left figure is in error and it should be 1/Z not Z, i.e. Z actually increases with temperature.
That is a really interesting observation. Does it mean in simple words there is a state between "good metal" (fermi liquid) and "bad metal" state: "resilient quasiparticles" state? And very naive connection with resistivity plot for organic superconductors: a hump ~100K is bad metal-resilient quasiparticles transition, and starting rho~T^2 (~50K) is a resilient quasiparticles-fermi liquid transition, am I wrong?
ReplyDelete/Andrew Bardin
Hi Andrew,
ReplyDeleteThis is a good question.
For the organics I think the relevant temperature ranges are
T < 20 K
Fermi liquid with T^2 resistivity
20 K < T < 50 K
Resilient quasi-particles
Drude peak in optical conductivity
Thermopower increases monotonically with temperature
Resistivity increases rapidly with temperature, faster than T^2
50 K < T < 100 K
bad metal
No Drude peak in optical conductivity
Thermopower DEcreases monotonically with temperature
Resistivity is larger than Mott-Ioffe-Regel limit
What causes the peak in resistivity at 100 K in the organics is controversial.
Some sample dependence is observed.
But DMFT calculations do give such a peak when close to the Mott transition