Seeking a new phase of matter in organic charge transfer salts

An important finding of recent cluster DMFT studies concerns the nature of the metallic state in the Hubbard model at half filling. Near the Mott transition it is found that the scattering rate is  anisotropic over the Fermi surface (a Fermi liquid with momentum space differentiation) just as it is in the doped Hubbard model.
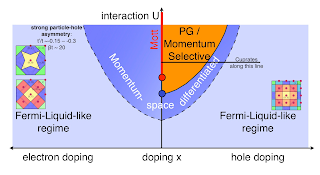
Emanuel Gull showed a general phase diagram (U/t vs. doping) in his talk at the Ringberg meeting.

(I could not find it in any of his papers, such as this PRB, but he kindly provided a copy). This "momentum space differentiated" phase is intermediate between the pseudogap state and the isotropic Fermi liquid, both as a function of doping and U/t.

This (temperature dependent) anisotropy should be observable in angle dependent magnetoresistance (ADMR) measurements on organic charge transfer salts in the kappa-(BEDT-TTF)2X family. These materials are all at half filling. A candidate material is X= Cu[N(CN)2]Br which lies close to the Mott transition. [By deuteration it can be tuned into the Mott phase]. Previous papers [e.g. see Section 3.4  in a recent review article I wrote with Ben Powell] have considered evidence for a pseudogap state in the organics. However, I am unaware of any significant attention being paid to this distinct idea of an anisotropic scattering rate in the organics.

In a 2007 PRL Singleton et al. found that that experimental data for X=Cu(SCN)2 can be adequately modelled by an isotropic scattering rate with a Fermi liquid temperature

dependence. Is the co-efficient for the quadratic temperature dependence consistent with what Dressel finds for the quadratic frequency dependence of the scattering rate  from

the optical conductivity? [This earlier post discusses the general issue of the relation between the temperature and frequency dependence of the scattering rate in Fermi liquid theory].

Thus, in order to see the variation in the scattering rate one may have to go even closer to the Mott insulating phase by considering X= Cu[N(CN)2]Br, (as in this Nature paper on the Nernst effect).