Deconstructing interlayer resistance

This posts presents a major theoretical challenge for the theory of strongly correlated electron materials. 

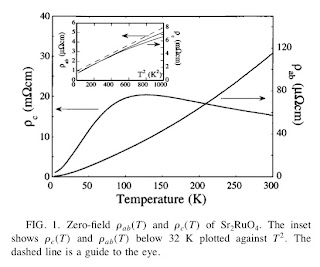
The graph below shows the temperature dependence of the interlayer and intralayer resistance of strontium ruthenate (Sr2RuO4). The inset shows that below 30 K both have the quadratic temperature dependence characteristic of a Fermi liquid. However, over a broader temperature range the interlayer resistance has a non-monotonic temperature dependence.   

The figure is taken from a 1998 PRB by Nigel Hussey and collaborators.
Although, there have been various "hand waving" explanations of this data, I am unaware of any actual calculation that reproduces it.

I see two possible alternative explanations which could be backed up by concrete calculations. (There are other alternatives but here I focus on the two least exotic and most doable theoretical scenarios).

1. The anisotropy may arises partly due to the presence of multiple bands at the Fermi energy and different coherence temperatures associated with them. Based on the interlayer hoppings deduced from LDA calculations and angle-dependent magnetoresistance oscillations [see this review by Bergemann et al.] the interlayer conductivity is dominated by the beta band [composed of d_xz and d_yz orbitals]. It needs to be checked if the following two conditions hold:

• the interlayer conductivity is dominated by a different band [because the corresponding Fermi velocity is much larger] than beta 
• if the beta band has a much lower coherence temperature [above which the crossover from a Fermi liquid to a bad metal occurs] than the other bands

If these conditions hold then I can conceive that one may find temperature dependences like that shown above. The relevant calculation would be a natural extension of the LDA+DMFT calculations described here.

2.  The anisotropic temperature dependence may arise for similar reasons as in the cuprates (see this post). The interlayer hopping integral vanishes in certain directions (along the zone diagonals) due to the crystal structure [see the Bergemann review], whereas the intra-layer Fermi velocity does not. Consequently, the interlayer conductivity is biased towards certain parts of the Fermi surface. If there is an anisotropic pseudogap or a very anisotropic scattering rate over the Fermi surface this may produce the desired anisotropy. This would require a Cluster DMFT type calculation on a realistic multiband model.