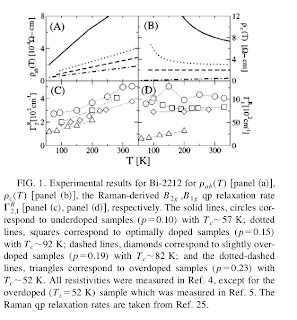
I just read a really helpful paper Optical symmetries and anisotropic transport in high-Tc transport by Tom Devereaux. Although the paper is a PRB it reads more like a short review. It is very clear and provides lots of summary expressions. The main purpose of the paper is to show the intimate connection between low-frequency electronic Raman scattering and charge conductivity. [n.b. this Raman scattering is NOT scattering off phonons but electron-hole pairs]. Furthermore, intra-layer and inter-layer conductivity can be related to Raman scattering of different symmetries [A1g, B1g, B2g]. The figure below shows this correlation.
I am hoping someone will do Raman experiments on organic charge transfer salts and see if they can see the anisotropic superconducting gap and possibly an anisotropic pseudogap
The expressions given could be used to calculate how the Raman response changes as there is a crossover from a bad medal to a Fermi liquid in a DMFT treatment of the Hubbard model.
The momentum dependence of the interlayer hopping [it vanishes in the nodal directions] is crucial for differences to occur between A1g and B1g scattering.
It is pointed out that the derived results for the A1g Raman and interlayer conductivity require that the intralayer momentum is conserved [at least partially] for interlayer hopping. This same condition is necessary for the observation of angle-dependent interlayer magnetoresistance, as discussed here.
Tom and Rudi Hackl also have an exhaustive Reviews of Modern Physics article, Inelastic light scattering from correlated electrons.
It is possible to define scattering rates associated with the electronic scattering and to relate these to scattering on the Fermi surface in the nodal and anti-nodal directions. This allows a comparison to be made with the temperature dependence predicted by "cold spot", "hot spot", and marginal Fermi liquid models for the anisotropy in the scattering rate.
I am hoping someone will do Raman experiments on organic charge transfer salts and see if they can see the anisotropic superconducting gap and possibly an anisotropic pseudogap
The expressions given could be used to calculate how the Raman response changes as there is a crossover from a bad medal to a Fermi liquid in a DMFT treatment of the Hubbard model.
The momentum dependence of the interlayer hopping [it vanishes in the nodal directions] is crucial for differences to occur between A1g and B1g scattering.
It is pointed out that the derived results for the A1g Raman and interlayer conductivity require that the intralayer momentum is conserved [at least partially] for interlayer hopping. This same condition is necessary for the observation of angle-dependent interlayer magnetoresistance, as discussed here.
Tom and Rudi Hackl also have an exhaustive Reviews of Modern Physics article, Inelastic light scattering from correlated electrons.



No comments:
Post a Comment