A gap without a gap

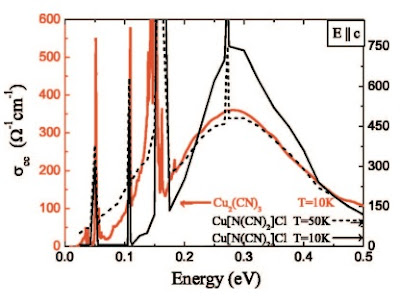
The above figure (taken from this PRB by Istvan Kezsmarki et al.) compares the frequency dependent conductivity in two Mott insulators, kappa(BEDT-TTF)2X with X = Cu[N(CN)2]Cl and X=Cu2(CN)3.

The former has a ground state with Neel antiferromagnetic order and clearly has an energy gap of about 0.1 eV.

In contrast, the latter compound may have a spin liquid ground state and has a much smaller energy gap, if any.

[The sharp peaks are due to intramolecular vibrational modes and not the electronic degrees of freedom.] Indeed it has been suggested that in the former compound

there is a charge gap, but that in the latter compound the optical conductivity has a power law dependence at low frequencies.

Note, that the charge gap [the change in the ground state energy when an electron is added or subtracted from the system](a signature of a Mott insulator) is a different physical quantity from the optical gap [the difference in energy between the ground state and the lowest excited singlet state with a transition dipole moment from the ground state]. Hence, it is possible, at least in principle, that the former is non-zero

and the latter is zero.

However, the relative size of the energy gaps also presents a puzzle because one can might then argue that X = Cu[N(CN)2]Cl is further from the metallic phase than the other compound. But X = Cu[N(CN)2]Cl requires a smaller pressure to destroy the Mott insulating phase (300 bar versus 4 kbar), which seems to contradict the simple argument based on the size of the gaps.

Ng and Lee calculated the frequency dependence of the optical conductivity in a Mott insulating state which is a spin liquid with a spinon Fermi surface and described by a U(1) gauge theory. They find that there is a power-law frequency dependence at low frequencies due to the conductivity of the spinons. The spinons are charge neutral and so do not couple directly to an electromagnetic field. However, they couple indirectly because the external field induces an internal gauge field in order to maintain the constraints associated with the slave-rotor representation of the electrons.

Deducing whether the experimental data shown above does imply zero optical gap for the (CN)3 material could be made more rigorous by subtracting the vibrational

contributions. A robust procedure now exists for this [see this PRB from Martin Dressel's group] and has been applied in the analysis of the optical conductivity of other members of the kappa-(ET)2X family. The figure below [taken from this PRB] shows the results of such an analysis for various X which allow one to cross the Mott transition. The black dashed curve in the bottom panel should be compared to the X = Cu[N(CN)2]Cl data in the top panel.

I thank Istvan Kezsmarki for pointing out a few ambiguities in the first version of this post.