Dimensionless ratios for metals II: Kadowaki-Woods

Following up on my earlier post, one extremely useful ratio is the Kadowaki-Woods ratio, which was originially introducted to understand heavy-fermion compounds. In a Fermi liquid metal, at low temperatures (sometimes as low as a 1 Kelvin) the specific heat capacity is linear in temperature and the resistivity depends quadratically on temperature. (The corresponding co-efficients are denoted gamma and A). Kadowaki and Woods found that for a wide range of heavy fermion compounds the ratio of A to gamma squared was approximately the same. This is important because it was consistent with the idea that the dominant source of scattering (and resistivity) was due to electron-electron scattering and that these materials have a Fermi liquid ground state. Since then it seems whenever people measure a T squared resistivity for a strongly correlated electron material people put the coefficients on the plot, which ends up looking like this:
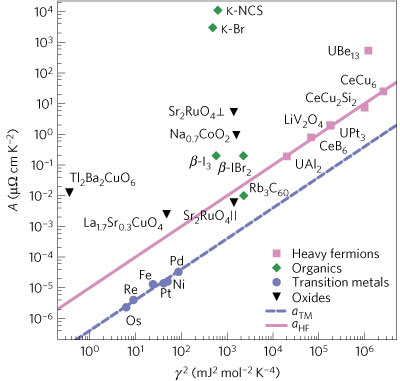
If points do not lie on the line then sometimes it is proposed that the electron-electron scattering is particularly large for the system is non-Fermi liquid. However, more thought is required as to what the real dimensionless ratio is that should be plotted. A paper just published in Nature Physics by my UQ colleagues Anthony Jacko, John Fjaerestad, and Ben Powell provides a definitive answer to this question. They find one needs to take into account the electron density and the spatial dimensionality of the system. The result is the following very impressive plot:


Note how the vertical scale covers resistivities varying by ten orders of magnitude! Hence, the authors have given a universal explaination using Fermi liquid theory for the low temperature resistivity in a diverse range of materials. This is a striking example of universality: where properties of a system are essentially independent of chemical and structural details.

One question I have is what the implications are of this analysis for some claims of non-Fermi liquid behaviour, especially near quantum critical points. For example, deviations from the Kadowaki-Woods ratio were used to characterise the breakup of heavy electrons near a quantum critical point.