Is there any difference in the nature of emergence in quantum and classical systems?
What is the difference between strong and weak emergence?
An emergent property of a system is one that is:
a. not present in the individual components of the system
b. difficult to predict
a priori from a knowledge of the components and their interactions
c. independent of the finer details of the components
Equivalently emergent properties are
a. qualitatively different
b. usually discovered empirically and sometimes are given a reductionist explanation
a posteriori
c. universal and stable to perturbations
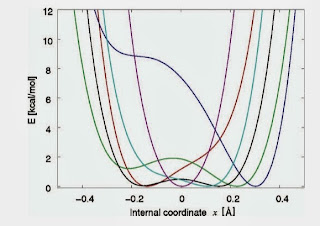
This can be illustrated with the rigidity of a solid
a. the individual atoms that make up a solid are not rigid.
b. elasticity theory preceded crystallography
c. all solids are rigid, regardless of their chemical composition.
Emergence occurs in both quantum and classical systems. The properties that emerge can be distinctly different. Superconductivity and superfluidity are intrinsically quantum.
However, the
associated issues and challenges: scientific, methodological, and philosophical are essentially the same. Emergence in classical systems is just as fascinating and challenging as for quantum systems.
Hence, last year I was surprised and disappointed to read the details of
The Physics of Emergence program at the Templeton Foundation.
It appears to be
based on two significant misunderstandings:
Emergence in quantum and classical systems is profoundly different.
In particular, quantum and classical emergence should be identified with strong and weak emergence, respectively.
I disagree with both the preceding two statements.
What is the difference between strong and weak emergence?
Some
philosophers equate these with ontological and epistemological emergence.
For practical scientists the issue boils down to the following possible
answers to the question, "Is it possible to predict emergent properties?":
i. No. It is impossible.
ii. No. But, one can make postdictions, i.e., once the phenomena has been observed very smart people can construct reductionist models that explain the phenomena. [BCS theory is an example].
iii. Yes. But, it is difficult. BECs and topological insulators give us hope.
iv. Yes. We just need a little more computer power and creativity.
The believer in strong emergence says i. All the other answers amount to weak emergence.
Different scientists will answer ii, iii, or iv.
I would probably go with ii.
The only scientist who I think might answer i. is Bob Laughlin on his more cantankerous days.
Yet i. appears to be serious option for many philosophers. This seems to be largely because of the thorny issue of consciousness.