Edge states define the bulk

Until thirty years ago the boundary of a quantum system was just considered an annoying irrelevance that one wanted to get rid of [or make as small as possible] so one could focus on the bulk properties.
However, the fractional quantum Hall effect and more recently topological insulators have shown that the boundary [edge] can actually tell us something fundamental about the bulk and is interesting in its own right.

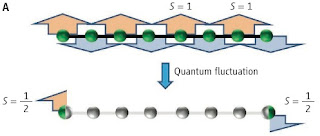
There is a nice Perspective in Science Symmetry meets topology by Xiao-Ling Qi. It introduces recent work by Xiao-Gang Wen and collaborators. They have used cohomology to classify symmetry protected topological states. A nice example is provided by the Haldane spin-1 antiferromagnetic chain. The bulk has an energy gap, but it has the highly  non-trivial property that a finite chain has spin-1/2 excitations at the ends [This PRL reports experimental evidence]. Hence, the edges characterise the unusual properties of the system.

Wen also has a helpful review on the arXiv which provides a gentle introduction to topological order. It is fascinating, but to me it highlights that in two dimensions we are still a long way from clear material realisations and definitive experimental signatures.