Deconstructing the Hall coefficient in strongly correlated metals

In basic solid state physics one learns that in metals sign of the Hall voltage is related to the sign of the charge carriers and the Hall coefficient is a measure of the density of the charge carriers, and is essentially temperature independent. However, in strongly correlated metals the situation is more complicated. Today I read a beautiful 1991 paper by N.P. Ong where he derives a simple geometrical interpretation of the transverse conductivity sigma_xy for a two-dimensional metal. It is proportional to the area swept out by the scattering length [Fermi velocity * scattering time] as one traverses the Fermi surface.

This result is based on a solution to the Boltzmann equation and so assumes a quasi-particle picture. Ong's result can be used to decipher the relative contributions from

• the curvature of the Fermi surface
• the Fermi surface area to circumference ratio
• variation in the scattering rate at different points on the Fermi surface

The latter can be responsible for significant temperature dependence of the Hall coefficient and the Hall angle.

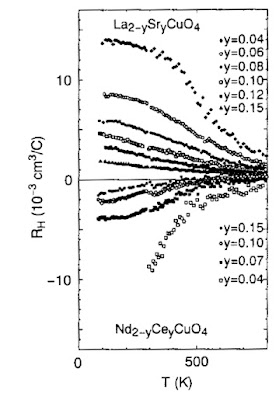
The figure above [taken from this review by Kontani] shows the temperature dependence of the Hall coefficient for cuprates at different dopings. The top and bottom are hole doped and electron doped respectively. The challenge for theory is to explain this strong doping and temperature dependence, which some claim goes beyond any Fermi liquid picture.