The Ising model is emblematic of “toy models” that have been proposed and studied to understand and describe emergent phenomena. Although originally proposed to describe ferromagnetic phase transitions, variants of it have found application in other areas of physics, and in biology, economics, sociology, neuroscience, complexity theory, …
Quanta magazine had a nice article marking the model's centenary.
In the general model there is a set of lattice points {i} with a “spin” {sigma_i = +/-1} and a Hamiltonian
The Ising model illustrates many key features of emergent phenomena. Given the relative simplicity of the model, exhaustive studies since its proposal in 1920, have given definitive answers to questions often debated about more complex systems. Below I enumerate some of these insights: novelty, quantitative change leads to qualitative change, spontaneous order, singularities, short-range interactions can produce long-range order, universality, three horizons/scales of interest, self-similarity, inseparable horizons, and simple models can describe complex behaviour.
Most of these properties can be illustrated with the case of the Ising model on a square lattice with only nearest-neighbour interactions (J_ij = J). Above the critical temperature (Tc = 2.25J), and in the absence of an external magnetic field the system has no net magnetisation. Below Tc, at net magnetisation occurs. For J > 0 (J < 0) this state is ferromagnetic (antiferromagnetic).
Novelty
The state of the system below Tc is qualitatively different than that at very high temperatures or the state of a set of non-interacting spins. Thus, the non-zero magnetisation is an emergent property, as defined in this post. This state is also associated with spontaneous symmetry breaking and more than one possible equilibrium state, i.e., the magnetisation can be positive or negative.
Quantitative change leads to qualitative change
The qualitative change associated with formation of the magnetic state can occur with a small quantitative change in the value of the ratio T/J, i.e., either by decreasing T or increasing J. Formation of the magnetic state is also associated with the quantitative change of increasing the number of spins from a large finite number to infinity.
Singularities
For a finite number of spins all the thermodynamic properties of the system are an analytic function of the temperature and magnitude of an external field. However, in the thermodynamic limit, these properties become singular at T=Tc and h=0. This is the critical point in the phase diagram of h versus T. Some of the quantities, such as the specific heat capacity and the magnetic susceptibility, become infinite at the critical point. These singularities are characterised by critical exponents, most of which have non-integer values. Consequently, the free energy of the system is not an analytic function of T and h.
Spontaneous order
The magnetic state occurs spontaneously. The system self-organises. There is no external field causing the magnetic state to form. There is long-range order, i.e., the value of spins that are infinitely apart from one another are correlated.
Short-range interactions can produce long-range order.
Although there is no direct long-range interaction between spins, long-range order can occur. Prior to Onsager’s exact solution of the two-dimensional model, many scientists were not convinced that this was possible.
Universality
The values of the critical exponents are independent of many details of the model, such as the value of J, the lattice constant and spatial anisotropy, and the presence of small interactions beyond nearest neighbour. Many details do not matter. This is why the model can give a quantitative description of experimental data near the critical temperature, even though the model Hamiltonian is a crude descriptions of the interactions in a real material. It can describe not only magnetic transitions but also transitions in liquid-gas, binary alloys, and binary liquid mixtures.
Three horizons/scales of interest
There are three important length scales associated with the model. Two are simple: the lattice constant, and the size of the whole lattice. These are the microscopic and macroscopic scale. The third scale is emergent and temperature dependent: the correlation length, i.e., the distance over which spins are correlated with one another. This can also be visualised as the size of magnetisation domains seen in Monte Carlo simulations.
The left, centre, and right panels above show a snapshot of a likely configuration of the system at a temperature less than, equal to, and greater than the critical temperature, Tc, respectively.
Understanding the connection between the microscopic and macroscopic properties of the system requires studying the system at the intermediate scale of the correlation length. This scale also defines emergent entities [magnetic domains] that interact with one another weakly and via an effective interaction.
Self-similarity
At the critical temperature, the correlation length is infinite. Consequently, rescaling the size of the system, as in a renormalisation group transformation, the state of the systems does not change. The system is said to be scale-free or self-similar like a fractal pattern. This is an example of self-organised criticality.
Inseparable horizons
I now consider how things change when the topology or dimensionality of the lattice changes or when interactions beyond nearest neighbours are added. This can change the relationships between the parts and the whole. Some details of the parts matter. Changing from a two-dimensional rectangular lattice to a linear chain the ordered state disappears. Changing to a triangular lattice with antiferromagnetic nearest-neighbour interactions removes the ordering at finite temperature and there are an infinite number of ground states at zero temperature. Thus, some microscopic details do matter.
The main point of this example is that to understand a large complex system we have to keep both the parts and the whole in mind. It is not either/or but both/and. Furthermore, there may be an intermediate scale, at which new entities emerge.
Aside: I suspect heated debates about structuralism versus functionalism in social sciences, and the humanities are trying to defend intellectual positions (and fashions) that overlook the inseparable interplay of the microscopic and macroscopic that the Ising model captures.
Simple models can describe complex behaviour
Now consider an Ising model with competing interactions, i.e. the neighbouring spins of a particular spin compete with one another and with an external magnetic field to determine the sign of the spin. This can be illustrated with the an Ising model on a hexagonal close packed (hcp) lattice with nearest neighbour antiferromagnetic interactions and an external magnetic field. The lattice is frustrated and can be viewed as layers of hexagonal (triangular) lattices where each layer is displaced relative to one another.
This model has been studied by materials scientists as it can describe the many possible phases of binary alloys, AxB1-x, where A and B are different chemical elements (for example, silver and gold) and the Ising spins on site i has value +1 or -1, corresponding to the presence of atom A or B on that site. The magnetic field corresponds to the difference in the chemical potentials of A and B, and is related to their relative concentration.
The authors studied the Ising model on the hexagonal close-packed (hcp) lattice in a magnetic field. The authors are all from materials science departments and are motivated by the fact that the problem of binary alloys AxB1_x can be mapped onto an Ising model. A study of this model found rich phase diagrams including 32 stable ground states with stoichiometries, including A, AB, A2B, A3B, A5B, and A4B3. Even for a single stoichiometry, there can be multiple possible distinct orderings (and crystal structures). Of these structures, six are stabilized by purely nearest-neighbour interactions, eight by addition of next-nearest neighbour interactions. The remaining 18 structures require multiplet interactions for their stability.
A second example is the Anisotropic Next-Nearest Neighbour Ising (ANNNI) model, which supports a plethora of ordered states, including a phase diagram with a fractal structure, known as the Devil’s staircase.
These two Ising models illustrate how relatively simple models, containing competing interactions (described by just a few parameters) can describe rich behaviour, particularly a diversity of ground states.
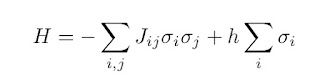





No comments:
Post a Comment