Best wishes for the New Year! One thing I hope to achieve this year is an actual understanding of things "Bayesian".
I am particularly interested because it gives a way to be more quantitative and precise about some of the intuitions that I use in science. For example, I tend to be skeptical of new experimental results (often hyped) that claim to go against well-established theories, regardless of how good the "statistics" of the touted result.
In this vein, Phil Anderson argued that Bayesian methods should have been used to rule out the significance of "discoveries" such as the 10 keV neutrino and the fifth force. In 1992 he wrote a Physics Today column on the subject.
An interesting metric for mathematical formula is the ratio of profound and wide implications to the simplicity of the formula and its derivation. I suspect that Bayes' formula for conditional probabilities would win first place!
P(A|B) denotes the probability of A given B.
The proof takes about two lines. If you multiply both sides of the equation about by P(B) the identity holds because both sides of the equation are just different ways of writing P(A and B).
My first attempt to understand the applications and implications of Bayes was reading the relevant sections in Phil Nelson's beautiful book, Physical Models of Living Systems. There is a helpful section entitled, "Bayes formula provides a consistent approach to upgrading our degree of belief in light of new data."
More recently, I found this wonderful and short video very helpful, as it clearly defines terms, uses graphical representations, and gives some concrete examples.
A Bayesian perspective highlights the importance of reporting negative results and is the basis of a seminal paper
Why Most Published Research Findings Are False by John P. A. Ioannidis
A measure of the profundity of Bayes is that the Stanford Encyclopedia of Philosophy has two articles on the topic
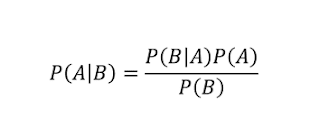




No comments:
Post a Comment