Superconductivity in kagome metals

Condensed matter physics is driven by fashion (too much). Is it fair to say that the latest fashion is the vanadium-based kagome metals  AV3Sb3 (A=K,Rb,Cs)?

[The PRL reporting superconductivity was published less than six months ago and has already been cited 44 times.]

These are certainly fascinating materials and have probably attracted attention for the following reasons.

-Kagome lattices support rich physics such as flat bands, Dirac metals, massively degenerate ground states, and (possibly) spin liquids.

-unlike other Kagome metals these compounds have both inversion and time-reversal symmetries, there is a Z2 topological invariant associated with bands near the Fermi surface, and topologically non-trivial surface states

-they are superconducting; furthermore, there are two superconducting domes as a function of pressure

-an anomalous Hall effect has been observed, which may result from topological physics

-there may be several types of charge order, including chiral charge density wave order

-the materials may be a topological superconductor [which MAY mean that it can be used to construct qubits that are "topologically protected].

Here are a few papers that I have looked at to get a better feel for this topic. I add a few things I gleaned from the papers and some basic questions I have. I welcome suggestions of other papers, that may be more helpful introductions. 

CsV3Sb5: A Z2 Topological Kagome Metal with a Superconducting Ground State 

Brenden R. Ortiz, Samuel M. L. Teicher, Yong Hu, Julia L. Zuo, Paul M. Sarte, Emily C. Schueller, A. M. Milinda Abeykoon, Matthew J. Krogstad, Stephan Rosenkranz, Raymond Osborn, Ram Seshadri, Leon Balents, Junfeng He, and Stephen D. Wilson

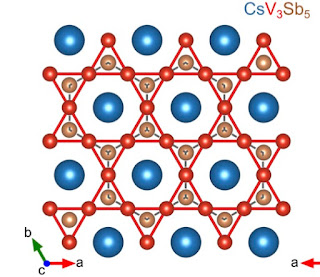
The figure below shows a top-down view of a single layer. The V atoms (red) form a Kagome lattice. There are three V atoms per unit cell.

The authors present DFT-based band structure calculations, which are compared to ARPES data. The good agreement suggests to me that strong correlations are not important. 

The authors use their band structures to construct Wannier orbitals and a tight-binding model for the band structure. However, even in the Supplementary information, they provide no details of this. I would like to know answers to the following.

For bands near the Fermi energy what is the composition of the underlying atomic orbitals (especially, how much d on V and p on Sb)?

How much of the band structure is described by a simple tight-binding model on a Kagome lattice with only next-nearest neighbour hopping?

Is the hopping between V sites via the p orbitals on the intermediate Sb atoms (superexchange in chemistry language)?

What is the band filling? 

Simple charge counting suggests there is one electron per triangle (1/6 band filling).

At a temperature of 100 K the intralayer resistivity is about 10 microohm-cm, well below the Mott-Ioffe-Regel limit (where the mean-free path is comparable to the lattice spacing), also suggesting that strong correlations are not significant.

Electronic instabilities of kagome metals: saddle points and Landau theory Takamori Park, Mengxing Ye, Leon Balents

Section V. A. discusses a tight-binding model. I think it is for the Kagome lattice with only nearest-neighbour hopping.

Double-dome superconductivity under pressure in the V-based Kagome metals AV3Sb5 (A = Rb and K)

C. C. Zhu, X. F. Yang, W. Xia, Q. W. Yin, L. S. Wang, C. C. Zhao, D. Z. Dai, C. P. Tu, B. Q. Song, Z. C. Tao, Z. J. Tu, C. S. Gong, H. C. Lei, Y. F. Guo, S. Y. Li

Answers to the following questions may determine whether interest in these materials is sustained.

Is the superconductivity topological?

Is the superconductivity unconventional? There are two independent parts to this question: does the superconductivity result from electron-phonon coupling or purely electronic interactions? Is the order parameter s-wave?

[On the related question of whether there are nodes in the superconducting energy gap there are already preprints with contradictory conclusions].

Is there any significant connection between any of the following: the topological character of the metal, the superconductivity, charge density orderings, and electron correlations?