Bad metallic behaviour in ultracold atoms

There is a nice paper
Bad metallic transport in a cold atom Fermi-Hubbard system 
Peter T. Brown, Debayan Mitra, Elmer Guardado-Sanchez, Reza Nourafkan, Alexis Reymbaut, Simon Bergeron, A.-M. S. Tremblay, Jure Kokalj, David A. Huse, Peter Schaus, and Waseem S. Bakr

The paper represents a significant experimental advance in using ultracold atoms to investigate questions directly relevant to strongly correlated electron systems. In this case, the system Hamiltonian can be tuned to be a Hubbard model on a square lattice, such that the model parameters, U and t, and the doping, n are known.
One limitation is that current experiments can only be performed down to the lowest temperature of T/t =0.3. [For comparison, for cuprates this is of the order of 1000 K!].
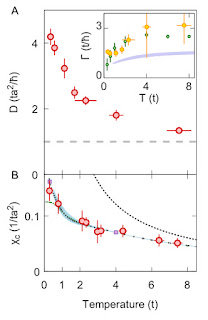
Using imaging techniques the authors are able to directly extract the density (charge) diffusion constant D and the density susceptibility, chi, shown below. The experimental data are red dots. The blue curve is the result of calculations based on the Finite Temperature Lanczos Method (FTLM). Green dots the results of Dynamical Mean-Field theory. Gamma is the density relaxation rate.

Both the experiment and the ability to make such a detailed comparison with concrete theoretical calculations is a significant and exciting achievement.

The dashed curve in the upper panel is the value of the diffusion constant associated with the Mott-Ioffe-Regel limit below which one expects bad metal behaviour.
Aside: one should always keep in mind that for the MIR limit, different authors use different criteria, leading to different factors of pi, sqrt(pi), ...

Using the Nernst relation, sigma = chi * D,  the data above gives the conductivity (sigma) and resistivity (rho), shown below.

The blue and green curves correspond to the predictions, of FTLM and DMFT, respectively. The dashed grey line is the Mott-Ioffe-Regel limit.

One comment I have concerns an additional comparison that the authors could make. Based on heuristic arguments and results from AdS-CFT, Hartnoll conjectured a lower bound for the diffusion constant, hv_F^2/T.
Previously, Nandan Pakhira and I showed that this bound was significantly violated in the bad metallic regime, as described by DMFT.

There is also a commentary on the paper by Ehud Altman at the Journal Club of Condensed Matter.
I thank Matt Davis for bringing the paper to my attention.