A basic but important skill: critical reading of experimental papers

Previously, I highlighted the important but basic skill of being skeptical. Here I expand on the idea.

An experimental paper may make a claim, "We have observed interesting/exciting/exotic effect C in material A by measuring B."
How do you critically assess such claims?
Here are three issues to consider.
It is as simple as ABC!

1. The material used in the experiment may not be pure A.
Preparing pure samples, particularly "single" crystals of a specific material of know chemical composition is an art. Any sample will be slightly inhomogeneous and will contain some chemical impurities, defects, ... Furthermore, samples are prone to oxidation, surface reconstruction, interaction with water, ... A protein may not be in the native state...
Even in a ultracold atom experiment one may have chemically pure A, but the actual density profile and temperature may not be what is thought.
There are all sorts of checks one can do to characterise the structure and chemical composition of  the sample. Some people are very careful. Others are not. But, even for the careful and reputable things can go wrong.

2. The output of the measurement device may not actually be a measurement of B.
For example, just because the ohm meter gives an electrical resistance does not mean that is the electrical resistance of the material in the desired current direction. There are all sorts of things that can go wrong with resistances in the electrical contacts and in the current path within the sample.
Again there are all sorts of consistency checks one can make. Some people are very careful. Others are not. But, even for the careful and reputable things can go wrong.

3. Deducing effect C from the data for B is rarely straightforward.
Often there is significant theory involved. Sometimes, there is a lot of curve fitting. Furthermore, one needs to consider alternative (often more mundane) explanations for the data.
 Again there are all sorts of consistency checks one can make. Some people are very careful. Others are not. But, even for the careful and reputable things can go wrong.

Finally, one should consider whether the results are consistent with earlier work. If not, why not?

Later, I will post about critical reading of theoretical papers.

Can you think of other considerations for critical reading of experimental papers?
I have tried to keep it simple here.

The joy and mystery of discovery

My wife and I went to see the movie, The Man Who Knew Infinity, which chronicles the relationship between the legendary mathematicians Srinivasa Ramanujan and G.H. Hardy. I knew little about the story or the maths and so learnt a lot. I think one thing it does particularly well is capturing the passion that many scientists and mathematicians have about their research, including both the beauty of the truth we discover and the rich enjoyment of the finding it.

The movie obviously highlights the unique, weird, and intuitive way that Ramanujan was able surmise extremely complex formula without proof.


I subsequently read a little more. There is a nice piece on The Conversation, praising the movie's portrayal of mathematics. A post on the American Mathematical Society blog discusses the making of the movie including a discussion with the mathematician Ken Ono, who was a consultant. Stephen Wolfram also has a long blog post about Ramanujan.

I enjoyed reading the 1993 article Ramanujan for lowbrows that considers some "simple" results that most of us can understand, such as the taxi cab number 1729.

The formula below features in the movie. It is an asymptotic formula for number of partitions of an integer n.

It is interesting that this is useful in the statistical mechanics of non-interacting fermions in a set of equally spaced energy levels, in the micro canonical ensemble.
Indeed it is directly related to the linear in temperature dependence of the specific heat and the (pi^2)/3 pre factor!

This features in Problem 7.27 in the text by Schroeder, based on an article in the American Journal of Physics. See particularly the discussion around equation 8, with W(r) replaced by p(n).

A Ph.D is more than a thesis

I recently met two people who got Ph.Ds from Australian universities who told me their stories. I found them disappointing.

Dr. A had a very senior role in government. After his contract ended he spend one year writing a thesis, largely based on his experience, submitted it and was awarded a Ph.D. He is now a Professor at a (mediocre) private university directing a research centre on government policy.

Dr. B was a software engineer. He worked part time and enrolled in a Ph.D in computer science. He would come on campus about once a month to meet his supervisor. As far as I am aware this was the only interaction he ever had with anyone from the university. He never went to any seminars, talked to other students, or took courses.

I don't doubt that on some level the theses submitted by these students may be comparable to those of other students and "worthy" of a Ph.D.
However, a colleague recently pointed out that at almost all universities the first page of the thesis says something like:

"A thesis submitted in partial fulfilment of the requirements for a Ph.D"

I think some of most important things you can learn in a Ph.D are not directly related to the thesis, as I discussed when arguing that the class cohort is so important.

A related issue is that I consider that undergraduates who skip classes yet pass exams are not really getting an education.

What is the chemical potential?

I used to find the concept of the chemical potential rather confusing.
Hence, it is not surprising that students struggle too.
I could say the mantra that "the chemical potential is the energy required to add an extra particle to the system" but how it then appeared in different thermodynamic identities and the Fermi-Dirac distribution always seemed a bit mysterious.

However, when I first taught statistical mechanics 15 years ago I used the great text by Daniel Schroeder. He has a very nice discussion that introduces the chemical potential. He considers the composite system shown below, where a moveable membrane connects two systems A and B. Energy and particles can be exchanged between A and B. The whole system is isolated by the environment and so the equilibrium state is the one which maximises the total entropy of whole system.

Mechanical equilibrium (i.e. the membrane does not move) occurs if the pressure of A equals the pressure of B.

Thermal equilibrium (i.e. there is no net exchange of energy between A and B) occurs if the temperature of A equals that of B. Thus, temperature is the thermodynamic state variable that tells us where two systems are in thermal equilibrium.

Diffusive equilibrium (i.e. there no net exchange of particles between A and B) occurs if the chemical potential of particles in A equals that in B, where the chemical potential is defined as

Starting with this one can then derive various useful relations such as those between the Gibbs free energy and the chemical potential (dG= mu dN and G=mu N).
Thus, the chemical potential is the thermodynamic state variable/function that tells us whether or not two systems are in diffusive equilibrium.

Doug Natelson also has a post about this topic. He mentions the American Journal of Physics article on the subject by Ralph Baierlein, drawing heavily from his textbook. However, I did not find that article very helpful, particularly as he mostly uses a microscopic approach, i.e. statistical mechanics. (Aside: the article does have some interesting history in it though).
I prefer to first  use a macroscopic thermodynamic approach before a microscopic one as, I discussed in my post, What is temperature?

Strong electron correlations in geophysics

There is some fascinating solid state physics in geology, particularly associated with phase transitions between different crystal structures under high pressure. This provides some interesting examples and problems when teaching undergraduate thermodynamics. One of many nice features of the text by Schroeder is that it has discussions and problems associated with these phase transitions.

However, I would not have thought that the electronic transport properties, and particularly the role of electron correlations, would be that relevant to geophysics. But, I recently learnt this is not the case. A really basic unanswered question in geophysics is the origin and stability of the earths magnetic field due to the geodynamo. It turns out that the magnitude of the thermal conductivity of solid iron at high pressures and temperatures matters. One must consider not just the relative stability of different crystal structures but also the relative contributions of electron-phonon and electron-electron scattering to the thermal conductivity.

There is a nice preprint
Fermi-liquid behavior and thermal conductivity of ε-iron at Earth's core conditions 
L. V. Pourovskii, J. Mravlje, A. Georges, S.I. Simak, I. A. Abrikosov

They report results that contradict those of a recent Nature paper that has now been retracted.
A few minor observations stimulated by the paper.

a. This highlights the power and success of the marriage of Dynamical Mean-Field Theory (DMFT)  with electronic structure calculations based on Density Functional Theory (DFT) approximations. It impressive that people can now perform calculations to address such subtle issues as the relative stability and relative strength of electronic correlations in different crystal structures.

b. The disagreement between the two papers boils down to thorny issues associated with numerically performing the analytic continuation from imaginary time to real frequency. This is a whole can of worms that requires a lot of caution.

c. Subtle issues such as the value of the Lorenz ratio (Wiedemann-Franz law) for impurities compared to that for a Fermi liquid turn out to matter.

d. I have semantic issues about the use of the term "non-Fermi liquid" in both papers. The authors associate it with a resistivity (for high temperatures) that is not quadratic in temperature. The system still has quasi-particles that adiabatically connect to those in a non-interacting fermion system, and to me it is a Fermi liquid.

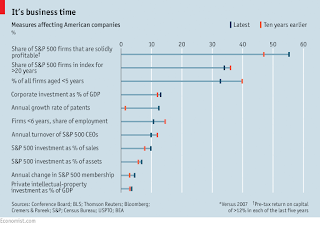
Whoosh.... Just how fast are universities changing?

The world is changing rapidly. It is hard to keep up. Companies boom and bust overnight... Rush .. New technologies disrupt whole industries... Whoosh....  People continually change not just jobs but field....  Universities need to look out..... They need to change rapidly.... The web is totally transforming higher education... Tenure is outdated... Focus on the short term... You may not survive... Whoosh...

This is a common narrative. But is it actually true?

Late last year, The Economist had an interesting article "The Creed of Speed: Is business really getting quicker?"

They look at certain objective quantitative measures to argue that the (surprising) answer to the question is no.
It is worth reading the whole article, but here a few snippets.
The graph below shows how little some measures have changed in the past 10 years.

More creative destruction would seem to imply that firms are being created and destroyed at a greater rate. But the odds of a company dropping out of the S and P 500 index of big firms in any given year are about one in 20—as they have been, on average, for 50 years. About half of these exits are through takeovers. For the economy as a whole the rates at which new firms are born are near their lowest since records began, with about 8% of firms less than a year old, compared with 13% three decades ago. Youngish firms, aged five years or less, are less important measured by their number and share of employment.

I love the line:

People who use dating apps still go to restaurants.

So there is a puzzle: people feel things are changing rapidly but they actually are not.

A better explanation of the puzzle comes from looking more closely at the effect of information flows on businesses. There is no doubt that there are far more data coursing round firms than there were just a few years ago. And when you are used to information accumulating in a steady trickle, a sudden flood can feel like a neck-snapping acceleration. Even though the processes about which you know more are not inherently moving faster, seeing them in far greater detail makes it feel as if time is speeding up.

I think that there is another reason why the perception of change is greater than the reality: the existence of a whole industry of consultants and managers whose (highly prosperous) livelihood depends on "change management". They spend a lot of time, energy, and money selling the "rapid change" and "impending crisis" line.

The article concludes by emphasising the importance of long term investments, particularly by large firms.

New technologies spread faster than ever, says Andy Bryant, the chairman of Intel; shares in the company change hands every eight months. But to keep up with Moore’s Law the firm has to have long investment horizons. It puts $20 billion a year into plant and R and D. “Our scientists have a ten-year view…If you don’t take a long view it is hard to keep your production costs consistent with Moore’s Law.” 

And what about Apple, with the frantic antics of which this article began? Its directors have served for an average of six years. It has invested heavily in fixed assets, such as data centres, which will last for over a decade. It has pursued truly long-term strategies such as acquiring the capacity to design its own chips. Mr Cook has been in his post for four years and slogged away at the firm for 14 years before that. Apple is 39 years old, and it has issued bonds that mature in the 2040s. 

Forget frantic acceleration. Mastering the clock of business is about choosing when to be fast and when to be slow. 

Now what about universities, particularly large ones with good reputations?

First, they are changing much more slowly than companies and much less susceptible to "market" pressures.
John Quiggin did a comparative study, entitled Rank delusions, of the list of leading US companies and leading universities over the last 100 years. In contrast, to the companies the university rankings are virtually unchanged.

Second, if you consider institutions such as Harvard, Oxford, Georgia Tech, Ohio State, Indian Institutes of Technology, University of Queensland, they all have in some sense a unique "market" share with few (or no) competitors, particularly with respect to undergraduate student enrolments, within a certain geographic region (country or state). It is a pretty safe bet that they will be just as viable twenty or thirty years from now. They are not going to be like Kodak.

There are certainly cultural changes, such as the shift from scholarship to money to status.

But, we should not loose sight of the fact that the "core business" and "products" are not changing much. With regard to teaching, I still centre my solid state physics lectures around Ashcroft and Mermin. I may sometimes use powerpoint and get the students to use computer simulations. But what I write on the whiteboard and the struggle for me to explain it and for students to understand it are essentially the same as they were 40 years ago (i.e. before laptops, smart phones, the web, ...) when Ashcroft and Mermin was written.

What about research?
Well good research is just as difficult as it was in pre-web days and before metrics and MBAs. It may be easier to find literature and to communicate with colleagues via email and Skype. But, these are second order effects...

So what are the lessons here?

Foremost, faculty and administrators need to have a long term view.
We should be skeptical about the latest fads and crisis and the focus on investing for the future.
Becoming a good teacher takes many years of practise and experience.
The most significant research requires long term investments in developing and learning new techniques, including many false leads and failures.
Real scholarship takes time.
It is the quality of the faculty, not the administrative policies or the slickness of the marketing, that make a great university.
Attracting, nurturing, and keeping high-quality faculty is a long and slow process that requires stability and long term investments.

What do you think?
How rapidly are things changing?
How much do we need to adapt and change?

The power of simple free energy arguments

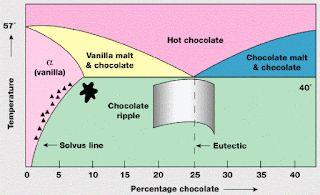
I love the phase diagram below and like to show it to students because it is so cute.

However, in terms of understanding, I always found it a bit bamboozling.

On monday I am giving a lecture on phase transformations of mixtures, closely following the nice textbook by Schroeder, Section 5.4.

Such a phase diagram is quite common.
Below is the phase diagram for the liquid-solid transition in mixtures of tin and lead.

Having prepared the lecture, I now understand the physical origin of these diagrams.

Eutectic [greek for easy melting] point is the lowest temperature at which the liquid is stable.

What is amazing is that one can understand these diagrams from simple arguments based on a very simple and physically motivated functional form for the Gibbs free energy that includes the entropy of mixing.

It is of the form

G(x) = C + D x + E x(1-x) + T [xlnx + (1-x)ln(1-x)]

where x is the mole fraction of the one substance in the mixture and T is the temperature.
The parameters C, D, and E are constants for a particular state.

The second term represents the free energy difference between pure A and pure B.
The third term represents the energy difference between A-B interactions and the average of A-A and B-B interactions. [I am not sure this is completely necessary].
The crucial last term represents the entropy of mixing (for ideal solutions).

Below one compares the G(x) curves for the three states: alpha (solid mixture with alpha crystal structure), beta, and liquid in order to construct the phase diagram.

Quantum limit for the shear viscosity of liquid 3He?

Next month I am giving two versions of a talk, "Absence of a quantum limit to the shear viscosity in strongly interacting fermion fluids." The first talk will be a UQ Quantum science seminar and the second at the Telluride workshop on Condensed Phase Dynamics. These are quite different audiences, but both will not be so familiar with the topic and so I need good background slides to introduce and motivate the fascinating topic.

The talk is largely based on a recent paper with Nandan Pakhira.

Here is one of the slides I am working on.

Some of the points I want to make here are the following.

There is experimental data on real systems.
This graph shows how for liquid 3He the shear viscosity varies by 3 orders of magnitude.

Here the shear viscosity decreases with increasing temperature (while the mean-free path gets shorter). This is counter-intuitive, a feature shared by dilute classical gases.

Fermi liquid behaviour is seen at low temperatures with the viscosity scaling with the scattering time (and mean free path) which is inversely proportional to T^2.

The last point is the most important.

At "high" temperatures, above the Fermi liquid coherence temperature (about 50 mK), the shear viscosity becomes comparable to the value n hbar (where n is the fluid density), which was conjectured by Eyring 80 years ago to be a minimum possible value.
This also corresponds to the Mott-Ioffe-Regel limit (where the mean free path is comparable to the inter particle spacing) (bad metal).

Aside: I still think it is amazing that when scaled with the density the viscosity [a macroscopic quantity] has the same units as Planck's constant. Just like h/e^2 is in ohms.

An earlier post considers similar issues for the unitary Fermi gas, that can be realised in ultra cold atom systems.

The big question addressed by the paper and talk is whether the comparable values are just a coincidence and whether by increasing the interactions you can go below the quantum limit.

The value of student pre-reading quizzes

How might you achieve some of the following desirable teaching goals?

• Get students to read the text book
• Find out what students are enjoying learning
• Find out what students are struggling to understand
• Keep students engaged
• Get feedback during the semester rather than at the end through student evaluations.

A key component of innovative teaching approaches such as peer assisted instruction, flipped classrooms, and just in time learning (a la Eric Mazur and Carl Wieman) are getting students before each class meeting to complete a short online quiz, based on reading the relevant part of the text. Ideally the teacher looks at the students answers before the class to get a feel for where they are at in understand and to address specific issues in the class.
Some of my UQ physics colleagues have really pursued this approach. 

I am currently teaching a second year undergraduate thermodynamics class with Joel Corney, from whom I have learnt a lot about teaching innovation.

Once a week the students complete a 3 question quiz on Blackboard (course software that all UQ courses "must" use). These do not contribute towards the final grade, but are a "hurdle" requirement: students must complete at least 70% to pass the course.
On average 80% of the students are completing these quizzes. In contrast, about 50% bother to show up for class.

The first two questions are brief basic comprehension questions base on the reading. e.g.,

Give a concise statement of the second law of thermodynamics for a system at constant temperature and volume. In your answer, refer only to system properties.

The third question is usually.

What concepts or topics did you find most difficult in the reading? If none, explain what you found most interesting.

I do find this is quite beneficial. I do believe that some of the goals above are achieved.
It does give me a much better feel for where the students are at. Some do appear to be doing the reading, thinking about it, and learning something. On the other hand, some are very confused. Others appear to not do the reading but just make wild guesses at the answers.

Below are some sample answers to the last question. The first two bring a smile to my face!

I loved how thermodynamics is used in so many areas in science. We studied Gibbs Free Energy in CHEM1100 so the term is familiar but it's fantastic to cover it in so much depth especially the mathematical reasoning behind the equations that were forced down our throat in first year with very minimal explanation. 

As an engineering student all this thermodynamic identity business does my noodle. Understanding all the theoretical stuff and "beautiful equations" is challenging coming from a world of plug and chug. 

It's really useful thinking about whether or not properties are intensive or extensive. It was always kind of a gut feeling type thing, but it's nice to finally clarify it. 

I feel like a lot of this stuff seems kind of useless at the moment, hopefully it will all fall into place soon. I know that it should be simple, but I can't seem to wrap my head around the free energy stuff and particularly how it is related to entropy.  

Fuel cells seem super cool. I don't particularly understand the Legendre transformations that were mentioned in the footer of page 157. 

I found it hard to keep up with the logic. Though i 'found the answers' to the questions above, i do not fully understand them. 

It's satisfying having the four thermodynamic potentials and identities but I feel like it's just a gateway to confusion, like all the assumptions that are made for the various derivatives of energy and entropy, etc.. Wizard 'diagrams' still don't help.

I struggled with the concept "free energy" until I really looked at the reading question. Having to think about it properly made me really understand what is meant by the term. I would still like to go over this concept in class. 

I am lost in the relationship between U, F, H and G. 

I know this is a physics course, but how much chemistry content is assumed knowledge?  

I don't get how in deriving the ds_total=-(1/T)dF form of the second law of thermodynamics for constant volume and temperature you can assume that the temperature of the system is equal to the temperature of the surroundings, and for there to still be an exchange of energy between the two. Unless its an isothermal transfer of heat between the system and surroundings, I don't get how you can have no temperature gradient, yet for there to be a transfer of energy between the system and environment in a no-work process. An explanation in the lecture would be greatly appreciated. 

i thought i understand the arguments, but i know i dont when i tried the questions.

This is very useful and helpful feedback.
However, the benefit comes with a cost... my time. It takes about 2-3 hours to read and grade the responses. Furthermore, you have to be well organised to do this before the lecture. (I didn't manage to do that for my first 2 weeks but have now caught up and so now hope to...)  If you want to change the lecture that also takes more time....
In a leisurely world what would be great would be to actually respond individually online to some of the student questions...

Learning from teaching experience

I recently spoke to a colleague who has now been teaching for three years. I asked her,
"What have you learned from the experience? What would you do differently? What advice do you have for new faculty members?"
Here is what she said.

"I taught too slowly and did not cover enough material. Students complained about this. I assumed the students had weaker background knowledge than they did. I should have taught at a more advanced level. The exams I set were too easy and too many students got high grades. I should not have done so many worked examples in class. I should not have spent so much class time answering students questions. I followed the text book closely. It would have been better to challenge the students more by drawing material from a range of sources."

If you think this is surprising, it is because everything I wrote above is a lie. I have never heard anyone say anything like that!
In fact, I always hear people say the exact opposite.
Yet we all seem slow to learn from our experience and the experience of others.

So here is useful advice, particularly for beginners.
Whatever you are thinking or planning,

• slow down
• cover less material
• don't assume students know or understand material from pre-requisite courses
• simplify everything (explanations, assignment and exam questions, assessment)
• keep repeating stuff
• give more examples
• listen to students questions and answer them
• follow a text closely
• make the exam questions clearer and easier

Lineage of the Janus god metaphor in condensed matter

Five years ago, Antoine Georges and collaborators invoked the metaphor of the greek god Janus to represent the "two-faced" effects of Hund's coupling in strongly correlated metals.

I wondered where they got this idea from: was it from someones rich classical education?
In the KITP talk, I recently watched online, Antoine mentioned he got the idea from Pierre de Gennes.

In his 1991 Nobel Lecture, de Gennes said

the Janus grains, first made by C. Casagrande and M. Veyssie. The god Janus had two faces. The grains have two sides: one apolar and the other polar. Thus they have certain features in common with surfactants. But there is an interesting difference if we consider the films which they make —for instance, at a water-air interface. A dense film of a conventional surfactant is quite impermeable. On the other hand, a dense film of Janus grains always has some interstices between the grains, and allows for chemical exchange between the two sides: "the skin can breathe. " This may possibly be of some practical interest.

Here are some images of "Janus particles".

How do you teach students that the details DO matter?

For some reason I have only become more aware of this issue recently.
I have noticed, particularly among weaker undergraduate students, a lack of concern about details.
This is not just among beginning undergrads but even final year students.

Here are some examples, from a range of levels.

Language.
Force, energy, and power are not the same thing.
Each refers to distinct physical concepts and entities.
Similarly, temperature, heat, internal energy, and entropy...
The wave function, potential energy, and probability....

Units.
Every physical quantity has well-defined units. You need to state them and keep track of them in calculations.

Significant figures.
These need to be justified and self-consistent.

Arguments and solutions to problems.
These need to be stated in a logical order. Assumptions and approximations need to be stated and justified.

The sloppiness is particularly evident in the exam papers of weaker students. One might excuse some because of the stress and rush of the situation. But, I also encounter some of the confusion and sloppiness in private discussions and assignments. Sometimes I fear they hope they can "bluff" their way towards some partial marks.

How does one address this issue?

I really don't know. I welcome suggestions.

One can certainly "nag" students about how the details do matter and penalise them in exams and assignments for sloppiness. However, this seems to have limited effect.