Has it been observed in solid state physics?
At the Journal Club of Condensed Matter, Patrick Lee has a very nice and helpful commentary, Observation of the chiral anomaly in solids, that highlights a preprint, based on a recent talk by Phuan Ong at the APS March meeting.
Later I hope to write more about the solid state physics, earlier work of which I have mentioned before.
I just want to highlight a beautiful and succinct paragraph from the preprint that explains why the chiral anomaly is so important in quantum field theory.
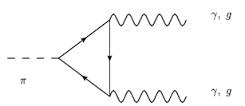
A bit of topological physics fell into quantum field theory (QFT) in the late 1960s [8–11]. The charged pions π± are remarkably long-lived mesons (lifetimes τ ∼ 2.3 × 10−8 s) because, being the lightest hadron, they can only decay by the weak interaction into muons and neutrinos via the processes π− → μ− + ν ̄μ and π+ → μ+ + νμ. Mysteriously, the neutral pion π0 decays much more quickly (by a factor of 300 million) even though it is a member of the same isospin triplet. Instead of the slow leptonic channels, π0 decays by coupling to the electromagnetic field Fμν in the process π0 → 2γ. The relevant diagram (shown below), called the Adler-Bell-Jackiw anomaly [8, 9], is a triangular fermion loop that links the π0 (the axial current) to the 2 photons (vector currents) [10, 11].
A hint of the topological nature of the anomaly is that the one-loop diagram receives no further corrections to all orders of perturbation theory. Subsequent research revealed that the anomaly expresses the breaking of a classical symmetry by quantum fluctuations. In modern QFT, the anomaly plays the fundamental role of killing unviable gauge theories [10, 11]. A proposed chiral gauge theory must be anomaly free. Otherwise it is not renormalizable. Arguably the most important example of the anomaly-free rule is the Glashow- Salam-Weinberg electroweak theory, in which the 4 triangle anomalies linking the lepton and quark doublets with gauge bosons sum exactly to zero within each generation. This fortuitous cancellation has been called “magical” [10].
A measure of the importance of this idea of anomaly cancellation is the fact that much of the initial string theory hype in 1980s arose because it was found that certain string theories with certain symmetry groups did have the sought after anomaly cancellations. See here for more.
Addendum (23 June, 2015): Peter Woit just posted about a recent talk "Anomalies Revisited" by Ed Witten.
The fundamental issue is that these are theories where the path integral does not determine the phase of the partition function. Part of story here is the well-known story of anomalies, perturbative and global. One interesting point Witten makes is that vanishing of these anomalies is not sufficient to be able to consistently choose the phase of the partition function, and he gives a conjecture for a necessary condition that is stronger than anomaly cancellation.
Witten discusses the specific case of three-dimensional massless Majorana fermions that may be realised in a topological superconductor.




Thank you for the great blog that I read all the time!
ReplyDeleteYou did not get to the question
"Has it been observed in solid state physics?"
I would like to know what your views on the experimental status are. To my mind the fact that a probably disorder induced large linear MR and symmetric hall/resistance channel mixing, muddies the waters in all named materials makes it very hard to believe that a combination of disorder , weird current paths or current jetting is not the leading candidate to explain small regions of negative MR behaviour.
I feel I am missing something because smarter minds than mine are making (cautious) claims.
Do you know of any predictions that are less common than negative longitudinal MR. Perhaps something like a predicted dependence of AMRO or some temperature dependence of the negative MR? Anything more than just negative MR to base such claims on?
Thanks for the kind comments about the blog. I am glad you enjoy it.
DeleteI did not comment yet on the solid state realisation yet because I wanted to first highlight the significance of the chiral anomaly for quantum field theory. Also, I am still trying to critically digest the experimental papers. I hope to write something soon.
Your caution and skepticism is wise and refreshing. One paper I looked at I found very unconvincing. It along the classic lines of a luxury journal paper: we see something weird so it must be this exotic effect.
On the other hand, the Xiong/Ong paper is more convincing because of the detailed angular dependence they do observe.
Thank you for the reassuring reply, I look forward to any views you have whenever (and if) you get a chance to post about it. It is very easy to make kind comments about the blog.
DeleteAt a time where the specific direction of a new physics beyond the Standard Model is far from clear, it is also worth pointing out that anomaly freedom is a useful "handmaiden (*)" to build quantum gauge field theories. (* I borrow this expression from an article by R. Brout, one of the father of the Higgs boson arxiv.org/pdf/hep-th/9706200.pdf).
ReplyDeleteNice blog Ross. I had just finished reading the P. Ong report you referred to when I came across your interesting blog. I have a deep fascination with the chiral anomaly, a fascination of which, unfortunately, exceeds my rather meager knowledge of QFT. And I was also struck by the comment, "Subsequent research revealed that the anomaly expresses the breaking of a classical symmetry by quantum fluctuations", which I see you also emboldened.
ReplyDeleteCould you be so kind as to explain that a little further in some detail? IOW, how quantum fluctuations achieve the breaking of (whatever) classical
symmetry, and why that is important.
PS I found refreshing your Biblical interests and comments , and Genesis video.
PSS. To address artfuldoger's skepticism I think P. Ong presents a pretty convincing case for separating Chiral anomaly in a Dirac semimetal from speculation based upon evidence of not only such a narrow (negative MR) current plume acutely aligned to E II B, but also upon the fact that the axial current is steered & locked to the B field rather than being pinned to the direction of the crystal axis. No?