The challenge of molecular crystal structure prediction

Garnet Chan gave a nice talk at the Condensed Phase Dynamics meeting about recent work on the problem of using computational methods to predict the crystal structure of organic molecular crystals. He began with the provocative statement of John Maddox, long-time editor of Nature, that

One of the continuing scandals in the physical sciences is that it remains impossible to predict the structure of even the simplest crystalline solids from a knowledge of their composition.

I previously posted about this "scandal".

Molecular crystals are particularly challenging because they often form polymorphs, i.e. several distinct competing crystal structures, that have energies differing on the scale of 1 kJ/mol [0.2 kcal/mol ~ 10 meV]. Calculating the absolute and relative energies of different crystal structures to this level of accuracy is a formidable challenge, going far beyond what is realistic with most electronic structure methods, such as those based on Density Functional Theory (DFT).

This problem is also of great interest to the pharmaceutical industry because the "wrong" polymorph of a specific drug can not only be ineffective but poisonous.

Aside: Polymorphism is also relevant to superconducting organic charge transfer salts. For example, for a specific anion X the a compound (BEDT-TTF)2X multiple crystal structures are possible, denoted by greek letters alpha, beta, kappa, ...  , with quite different ground states: superconductor, Mott insulator, metal, ...

There are two key components to the computational challenge of predicting the correct crystal structure:

1. having an accurate energy landscape function
2. searching the complex energy landscape to find all the low-lying local energy minima

Previously, it was thought that 2. was the main problem and one could use semi-empirical "force fields" [potential energy functions]. However, with new search algorithms and increases in computational power it is now appreciated that 1. is the main bottleneck to progress.

Sally Price has a nice tutorial review of the general problem here.

Every few years there is a crystal structure prediction competition where several teams compete in a "blind test". A report of the most recent competition is here.

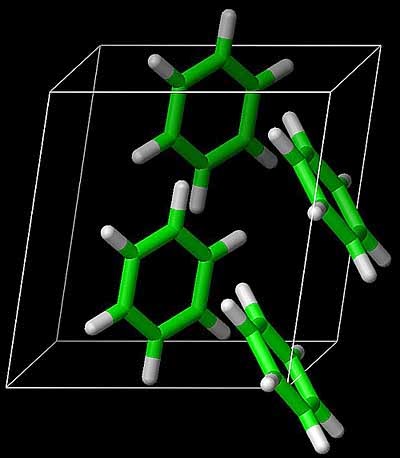
Garnet described recent work in his group [soon to be published in Science] using state-of-the-art  computational chemistry methods to calculate the sublimation energy of benzene [the hydrogen atom of organic molecular crystals].

It is essential to utilise two advances in computational chemistry from the last decade:
1. local correlation theories that use fragment expansions
2. explicit r12 correlation.

They obtain a ground state energy with an estimated uncertainty of about 1 kJ/mol.
This agrees with the measured sublimation energy, although there are various subtle corrections that have to be made in the comparison, including the zero-point energy.

Update. August 11, 2014.

The paper has now appeared in Science with a commentary by Sally Price.

Talk on Diabatic state models for methine dyes

Tomorrow I am giving a talk at the Condensed Phase Dynamics meeting in Telluride. The slides are here. It is largely based on two papers with Seth Olsen.

A three-state effective Hamiltonian for symmetric cationic diarylmethanes

A two-state model of twisted intramolecular charge-transfer in monomethine dyes

Significant advances in quantum chemical simulations of large systems

Yesterday at the Condensed Phase Dynamics meeting in Telluride there we nice talks by Eran Rabani and Todd Martinez highlighting recent advances they have independently made in simulating large systems. Rabani is largely concerned with solid systems such as silicon nanoparticles and Martinez with hundreds of reacting molecules.

Rabani's work with Roi Baer and Daniel Neuhauser is a highly creative and original stochastic approach to doing electronic structure calculations.  Instead of explicitly determining wave-functions [or Kohn-Sham orbitals in DFT] they use stochastic wave functions [a random phase is assigned to each point on a spatial grid] and compute one-particle expectation values as averages over the ensemble of stochastic wave-functions.

For Kohn-Sham Density Functional Theory they obtain sub-linear scaling of the computational cost with system size, as reported in this PRL. Some of the original problems with the approach [slow converge for systems involving weakly coupled sub-systems, e.g. a pair of buckyballs] are solved with an embedded fragment approach, as described in this recent preprint.

Over the past decade Martinez' group has pioneered the use of Graphics Processing Units (GPUs) [think computer games] for quantum chemistry calculations. The figure below from this recent paper highlights the computational speedup compared to conventional codes and architectures.

One can now do a DFT-based calculation of the energy of about one thousand water molecules in less than one minute. The bottle neck is the cubic scaling of diagonalisation routines.

Todd described recent work "discovering chemical reactions with the nano reactor".

Most quantum chemistry calculations require "knowing the answer" before you begin. i.e, you know the reactants and the products and you make certain guesses as to transition states between them. However, given a set of reactants is it possible to have an automated computational procedure that allows discovery of new products and the mechanisms for their production?
The answer is yes, and this represents a significant advance.

Todd presented dynamical simulations of a set of 100-300 atoms for 1 nanosecond at temperatures of about 1000-1500 K.

This high temperature is used to reduce the effects of non-covalent interactions and allow many reactions to proceed within a nanosecond.

Indeed, one does discover new reactants that one would not just predict based on a knowledge of "freshman" chemistry. Furthermore, one can find the reaction paths.

They have also simulated the famous and controversial Urey-Miller experiment aimed at producing amino acids [the building blocks of proteins] from simple initial reactants [water, methane, ammonia, hydrogen].
The simulation did find glycine is formed, and via three different reaction pathways.

Condensed phase dynamics in Telluride

Last night I was stranded at Denver airport en route to the bi-annual Condensed phase dynamics meeting at the Telluride Science Research Center.  This is the third time I have been to this wonderful meeting. Getting there can be a real hassle. But, then you look at the scenery and enjoy the science and it seems worth it.

Unfortunately, due to the travel delays I missed the first two talks, by Joe Subotnik and Nandini Ananth.

Dominika Zgid gave a chemist's perspective on "How to make dynamical mean theory quantitative". Some of her work was discussed in a my last post. Today she mostly discussed a generalisation of iterative perturbation theory as an "impurity solver" for DMFT problems with multiple orbitals. See this preprint.

Peter Rossky discussed quantum chemical simulations of exciton dynamics in conjugated polymers.

This was motivated by an experiment reported in Science that claimed evidence for quantum coherent transport of excitons along a polymer chain at room temperature. Several oscillations were seen in the fluorescence polarisation anisotropy  as it decays in about a picosecond. These oscillations were identified with quantum inference [Rabi oscillations] between different exciton states delocalised over the polymer chain.

It turns out the experimental results have a much more mundane explanation.
The simulations of Adam Willard and Rossky are of classical dynamics on the adiabatic excited state potential energy surface calculated from a parameterised PPP [Pariser-Parr-Pople] model [basically a Hubbard model with long-range Coulomb interactions. They see oscillations similar to those in the experiment and can identified simply with classical nuclear motion associated with the polymer backbone stretching [phonons] in response to photo-excitation.

Much-hyped experiments claiming to show quantum coherence in photosynthetic complexes, probably also have a similar classical explanation in terms of nuclear dynamics rather than electronic coherences. A concrete interpretation in terms of vibrational coherences is in this PNAS paper. My skepticism of these "quantum biology" experiments has been expressed in many earlier posts.

Hopefully, tomorrow I will blog about talks from Eran Rabani, Todd Martinez, and Dvira Segal.

Quantum chemistry meets dynamical mean-field theory

I often discuss these two topics, but in separate posts. But, both are concerned with strong electronic correlations; one in molecules and the other in solids.
Is it possible to bring them together in a mutually beneficial manner?

1. How could quantum chemistry of finite molecules benefit from DMFT?

This is considered in a PRL from Columbia.
An earlier post reviewed nice work that used LDA+DMFT to study myoglobin. [See also a recent PNAS].
Broadly, I think DMFT will be most appropriate and useful in molecular problems that look something like an Anderson impurity problem: a single metal atom with a fluctuating magnetic moment and/or valence that is coupled to a large number of approximately degenerate electronic states. Indeed myoglobin falls in this class.

2. How could DMFT treatments of solids benefit from quantum chemistry methods?

Three answers to are considered in a nice JCP by Dominika Zgid and Garnet Chan.

A. It provides a way/framework to extend quantum chemical methods (approximations) to infinite crystals. This is most naturally done in the discrete bath formulation of DMFT.

B. Any DMFT treatment requires an “impurity solver” to treat the associated Anderson impurity-problem. In the discrete bath formulation this is solved by exact diagonalisation [called full configuration-interaction (CI) by chemists] and significantly limits the bath to less than a dozen states. However, the hierarchy of quantum chemistry approximations [HF, CCSD, CAS-SCF, ....] provide an alternative “lower cost” means to solve the bath problem and increase the number of bath states and possibly improve convergence.

C. It allows one to go beyond current ab initio DMFT studies that are based on Density Functional Theory (DFT) and its associated problems. Furthermore, such studies involve a certain amount of
“double counting” of correlations that are hard to correct for in a systematic manner.

Zgid and Chan treat the specific problem of cubic solid hydrogen for several different lattice spacings a. Qualitatively, this is analogous to the Hubbard model at half-filling with varying U/t. As the lattice constant increases there is a transition from a weakly correlated metal to a strongly correlated metal [3 peaks in the single particle spectral function] to a Mott insulator.

In a 2012 PRB, Zgid, Chan, and Emmanuel Gull study a 2 x 2 cluster DMFT treatment of the two-dimensional Hubbard model. They found that solving the associated impurity problem with a finite bath with quantum chemical approximations such as CCSD [coupled cluster singles and doubles] CAS(2,2) [complete active space with two electrons in two orbitals] produced reliable results at a fraction of the computational cost of exact diagonalisation.

The case for universal undergraduate exams

My wife's brother-in-law recently introduced me to the idea of the Iron triangle of higher education: at the vertices are the competing demands of access, cost, and quality. Pulling on one corner produces tensions in the other. Furthermore, different stake holders [students, parents, faculty, administrators, politicians] will prioritise one vertex over the others.

Aside: the triangle is also discussed in other contexts such as health care.

There is a nice essay
Breaking Higher Education's Iron Triangle: Access, Cost, and Quality 
by John Daniel, Asha Kanwar, and Stamenka Uvalic-Trumbic

It partly focusses on the important and complex issue of the massive expansion and aspirations of university education in the majority world. But many of the issues apply to all countries.

One of the concrete proposals for evaluating/ensuring quality is separating examinations from teaching institutions. Common exams would be administered by independent authorities/companies [think GRE, Cambridge A-levels, TOEFL, ...]. I think the advantages of this are considerable

• uniform standards
• public accountability
• freedom from grade inflation and student whining
• faculty would be seen by students as allies rather than adversaries

The low standards of some institutions would be quickly revealed. These advantages greatly outweigh some of the weaknesses [lack of institutional autonomy and flexibility, difficulty of assessing experimental work, teaching to the exam, ...].

The first author Sir John Daniel, was head of Open University in the UK for a decade. It pioneered distance learning. Hence, he is qualified to talk about the recent fashion in MOOC's [Massive Online Courses]. A recent paper is reviewed here and contains the following wisdom:

We need a climate in which colleges and universities are less imitative, taking pride in their uniqueness. It’s time to end the suffocating practice in which colleges and universities measure themselves far too frequently by external status rather than by values determined by their own distinctive mission.

With regard to institutional measures of teaching quality he warns:

Institutions must distinguish between quality assurance procedures, which can easily become compliance focused, and real efforts to enhance quality. For example, evaluating a course, though required, is not sufficient. Quality enhancement will only take place when the lessons from evaluation are reflected in the next offering of the course. Institutional quality assurance structures and processes are important, but beware of making them an exercise in compliance or accountability, rather than process of learning and self-improvement that really improves quality.

Are USA universities in crisis?

I have only slowly come to realise the crisis facing US universities. A tipping point was the release this week in movie theatres of the documentary The Ivory Tower. Seeing that people are willing to pay money to watch a negative documentary suggests there is a ground swell of public concern.



A few other things that showed me the extent of the problem are the following.

The article, Universities on the Defensive, by Hunter Rawlings  a former President of Cornell, and currently the President of the Association of American Universities, a consortium of 60 of the leading North American universities.

The Seattle Times recently ran a front page story about the problems of mushrooming student debt and eight myths about why college costs so much.

My UQ economics colleague John Quiggin has a piece in The Chronicle of Higher Education discussing how inequalities in the US system reflect the broader inequality in society.

The table below, taken from another interesting article, Navigating Culture Shock in The Chronicle of Higher Education contrasts the relative resources of Stanford and nearby San Jose State University.

What does this have to do with Australia?
Recently, the government introduced major reforms of Australian universities, aimed at making them more like the US system. This seems to be based on two simplistic notions:

1. because the US has the best universities in the world if we copy some of the features of the US system [making it very expensive for students] then we are going to end up with some world-class universities.

2. deregulation and "free markets" always produce better outcomes.

My main criteria for research quality

How does one evaluate the quality of ones own research and that of others?
First, acknowledge that this is subjective. Different people have different values, personalities, and background. Here are my values. Most are somewhat interconnected. Not only is the selection of criteria below subjective but how one evaluates each one is subjective and personal.

Validity.
Ultimately science is about truth and reality. How confident can I be that the results (but also conclusions) actually are correct? Are the results likely to be reproduced? Are they consistent will earlier work and general principles?
Of course, one can never be completely confident, but particularly with experience, once is able to weigh up the probability that results will stand the test of time. The more extra-ordinary the claims the greater the evidence must be.

Reality.
Ultimately, theories must have something to do with real materials and be experimentally testable in some broad sense. Research that claims to have technological relevance must have some chance of being actually realisable on the time scale of a decade or two and not wishful thinking and marketing [science fiction].

Concreteness.
There is a well defined problem. The research presents a well defined answer. For some papers/talks/grants I encounter it is not clear what the problem and answer are. It just seems like a bunch of measurements or a bunch of calculations. Uncontrolled approximations and poorly understood experimental techniques have some role, but do not have the same value as definitive techniques and results where one actually knows what one is doing.

Importance.
One measure of this is the breadth of application [or scientific relevance] and implication. Will this change how we think about a field? Will it make possible new measurements or new calculations? Does it solve an outstanding problem that has previously confounded excellent scientists?

Clarity.
For some work I am just never really clear what is being done, whether it is valid, or why it is important. On the one hand, this might just be because I don't have the relevant background to appreciate the work. On the other hand, I fear some scientists just don't make the effort to explain what they are really doing, the context, the assumptions, or the significance of their work.

I think that technical prowess, originality and priority are over-rated. There are exceptions. Sometimes they are very important, but they don't have intrinsic merit, and sometimes fail on the importance criteria.

Note that I do not consider funding, status [journals and institutions], or citations as good measures of research quality. They are sometimes a consequence of some of the above, but they are neither a necessary nor a sufficient condition for high quality research.

I welcome comments and discussion.

Deconstructing enzyme mechanism

Enzymes are amazing molecules. They increase rates of specific chemical reactions by factors as large as a trillion. Without them there would be no biochemistry and no life. Exactly, how they work remains controversial. Broadly they significantly lower the energy of the transition state for a chemical reaction and thus lower the activation energy, Ea. Since the reaction rate scales with
exp(-Ea/k_B T), lowering the barrier by one electron volt (23 kcal/mol) has a dramatic effect.

But, how is this lowering of the transition state achieved? There is no doubt that simple electrostatic effects can make a major contribution, as emphasised by Ariel Warshel. From the point of view of quantum physics, this is rather "boring". But, thats good science: going with the best and simplest explanation.
However, that is not the whole story, and particularly not for all enzymes.

One enzyme that is attracting significant interest is (KSI) keto-steroid isomerase, highlighted by nice work from the groups of Steve Boxer and Daniel Herschlag at Stanford. This enzyme catalyses the conversion of cholesterol into steroids such as oestrogen and testosterone.

Understanding has advanced by clever studies performing mutations [replacing specific amino acids in the protein by others] and replacing the reactant with a simpler phenol group with tuneable acidity, and seeing how the enzyme structure and catalytic power change.
Here are two short commentaries that put that work in context.

What Governs Enzyme Activity? For One Enzyme, Charge Contributes Only Weakly 
Richard Robinson

 Biochemistry: Enzymes under the nanoscope 
Anthony J. Kirby and Florian Hollfelder

The figure below [taken from the second commentary] how the substrate [reactant] is hydrogen bonded to two tyrosine [amino acids] molecules. The hydrogen network is crucial to the stabilisation of the transition state (middle panel).

That commentary emphasises how small changes in the hydrogen bond lengths [as little as 0.1 Angstroms] produce significant changes in the enzyme catalytic power. But, even engineering such a
small decrease is difficult.

This result has wide-reaching implications: it defines experimentally the distance scale on which enzymes can distinguish geometric rearrangements of atoms, and determines the energetic consequences of this constraint. The picometre-precision of KSI also explains why protein engineering to produce enzymes that have new or altered functions has proved so difficult.

The last statement refers to the grand challenge of trying to do "bio-mimetics" and produce artificial catalysts that could have the incredible power of enzymes.

This structural sensitivity also prevents a significant challenge to structural biology [a.ka. protein crystallography] and computational molecular modelling.  Distance resolutions of 0.1 A are at the boundary of the best protein X-ray crystallography. For  hydrogen bonds density functional theory based calculations are not that reliable on this length scale. Classical molecular dynamics cannot even describe moderate to short bonds.

I am particularly interested in KSI because of the presence of short to medium strength hydrogen bonds in which quantum nuclear effects play a role. The figure below is taken from this paper.

For such bonds changes in H-bond lengths of 0.1A can produce significant changes in the proton transfer potential. 

Furthermore, the interpretation of hydrogen-deuterium isotope substitution experiments will be complicated by the secondary geometric isotope effect.

The funny side of tenure

It is hard to get a permanent job, even for Sheldon Cooper!
In some departments when a tenured or tenure-track job opens up there are many internal candidates who have been waiting for this day. Then the machinations and angst begins....

On the plane to the USA I discovered there is a funny episode of The Big Bang Theory, Tenure Turbulence, which details with a scenario like that above of competing internal candidates.

Talk on quantum hydrogen bonds for chemists

Tomorrow I am giving a talk "Effect of quantum nuclear motion on hydrogen bonding" in the Chemistry Department at Stanford. My host is Tom Markland. Here are the slides. Much of the talk is based on this recent paper.

Note that some of the talk is different to one I gave last week in the physics department at UQ. It is important to gear any talk to the backgrounds and interests of the audience.

Government reforms of Australian universities

The Australian government recently announced some major reforms of the funding of universities. Students will have to pay more themselves and universities will be allowed to set tuition at the level they want. As before, tuition is paid for by a loan scheme (HECS) that students only pay back in taxation after they start earning above a threshold amount. Interest on the loans will higher than before.

Here are a couple of responses from Australian academics.

Nobel laureate Brian Schmidt has an article in today's Australian

Students should not shoulder the burden
He highlights one of the "dirty secrets" of the Australian system.

Student fees are a one-size-fits-all system, where every university gets the same amount of income, This system, after the uncapping of the number of student places allocated to each university in 2012, has led to the perverse incentive that rewards the teaching of large numbers of students at the lowest possible cost. Revenue raised from fees then can be used to cross-subsidise research. This is important for a university because its esteem is almost entirely set by international measures of its research quality. 

This funding model is so irrational that the status quo is unacceptable. Students suffer poor teaching outcomes, universities’ ability to undertake research is moderated by the number of undergraduates they attract rather than the quality of research, and we end up with sub-optimal teaching and research outcomes.

UQ economist Paul Fritjers has a cutting post on the Core Economics blog
What are the likely consequences of HECS fee liberalisation?
Here is an extract:

In terms of the impact of these reforms on ‘academia’, ie on ‘communities of scholars dedicated to truth finding’, I am less pessimistic than most of my colleagues. Whilst academic values will be entirely unwelcome and ousted from undergraduate degrees, simply because independent academics are seen as a potential threat to students, the even greater importance of research excellence will mean that academics will retain and expand their own little playgrounds in the graduate education and research realms: academia will simply become even more divorced from undergraduate education, which will become more and more like an extension of secondary school.

Update (August 15). I recently came across Joseph Stiglitz's warnings about Australia mimicking the USA.

Classification of topological orders

Quantum many-body states such as quantum Hall states, spin liquids, and topological insulators differ from superconductors, superfluids, and anti-ferromagnets in that they do not exhibit spontaneously broken symmetries. The latter is a major organising principle of quantum condensed matter: the broken symmetry can be used to distinguish different states and leads to new low-energy collective excitations (Goldstone bosons).

So, how does one characterise and categorise different states without broken symmetries?

Topological order has been proposed by Xiao-Gang Wen to be the relevant organising principle.
An earlier post considered the role of edge states in such a classification.

How does topology enter?
1. Consider a fractional quantum Hall system on different surfaces with different genus (sphere, torus, connected donuts, ...). Then the ground state is degenerate (in the thermodynamic limit) and the degeneracy depends on the genus of the surface.
In contrast, if one considers a two dimensional non-interacting gas of fermions, there is a unique ground state on both a sphere and a donut (plane with periodic boundary conditions).
2. For a system with an energy gap to the lowest excited state one can have edge states (low energy excitations that are spatially confined to the edge of the sample) and these are described by a topological field theory. [I am hazy on what this means; something like that the coupling constant in the action can have only integer values; these depend only on the topology of the space time.]

At the cake [weekly UQ condensed matter] meeting we are struggling with the paper
Local unitary transformation, long-range quantum entanglement, wave function renormalization, and topological order

Here are a few of the things I have learnt.

I think this is only about gapped states, i.e, where there is a non-zero energy gap to the lowest excited state.

Broadly the topologically ordered states are divided into two classes, depending on whether they have short- or long-range quantum entanglement. The former means that one can perform a set of spatially localised unitary transformations that map the state into a product (i.e. non-entangled) state.

Class I. Long-range entanglement
Topological order is "stable" (i.e. adiabatically connected) to any perturbation of the Hamiltonian.
Examples: fractional quantum Hall states, chiral spin liquids, Kitaev's toric code, topological Mott insulators. Topological superconductors (e.g., a p+ip state) are in this class but also spontaneously break symmetry too.

Class II. Short-range entanglement
Symmetry-protected topological order. This means only "stable" (i.e. adiabatically connected) to perturbations of the Hamiltonian that preserve a specific symmetry.
Examples: Haldane and AKLT phases of Heisenberg spin-1 antiferromagnetic chains, topological insulators.

The paper goes on to consider how for tensor product states one can define renormalisation group flows that will lead to a fixed point which will reveal a "simpler" wave function that can be classified in terms of the several tensors with many indices [provided the relevant symmetry groups are finite dimensional].

I welcome corrections and clarifications.

Teaching undergraduates about quasi-particles

When I first learnt and later taught solid state physics the concept of a quasi-particle only came up in the context of Fermi liquid theory.
Yet, quasi-particles are a profound and central concept of quantum many-body theory. Hence, it is important that students be exposed to this idea as soon and as much as possible.
I probably slowly started to appreciate this by looking at Phil Anderson's classic Concepts in Solids. It is based on lectures given at Cambridge in 1961-2, and inspired Josephson to invent his effect.
The second half of the book is all about quasi-particles.

So when teaching "Ashcroft and Mermin" there are several distinct opportunities to introduce quasi-particles, besides in the context of Fermi liquid theory.
These are holes, phonons, and magnons in a ferromagnet.
The case of holes I discussed earlier.
I was both embarrassed and pleased that when I taught magnons this year, one of the students asked, "Aren't these quasi-particles?"

For phonons I have a confession. In the solid state course we currently "skip" the whole subject. We just can't find the space/time. I feel things like Fermi liquid theory, semiconductors, magnetism, and superconductivity are more important. The students learn a little about phonons in an earlier statistical mechanics course.
There is some irony in me skipping the topic. When I first came to UQ for a job interview I had to give a lecture to a live undergrad class. The assigned topic was phonons in the solid state course.

Translating bureaucratic jargon

To support the move to online mode, an extensive communication and change management process is being developed in consultation with stakeholders and UQ-wide communities

I had to read this several times. Does this mean "we are going to tell everyone concerned what is happening" ?

On a related note, in the Times Higher Education Supplement there is a provocative article A very Stalinist management model that compares current practices in UK universities to those in Stalin's Russia. The author, Craig Brandist is Professor of cultural theory and intellectual history in the Department of Russian and Slavonic studies within the University of Sheffield. In the print edition the article title was "My Rallies of Endeavour Will Ensure the Impact Our Dear Leaders Desire." 

Quantum science seminar on hydrogen bonds

Each week at UQ there is a Quantum Science seminar. This is attended by people working in cold atoms, quantum information, condensed matter, quantum optics, and quantum engineered systems, mostly theorists. I am giving the seminar this week. I endeavoured to write an abstract that might be attractive and comprehensible to a broad audience. Here it is

The effect of quantum nuclear motion on hydrogen bonding

Most of chemistry can be understood by treating the atoms in molecules as classical particles. Quantum zero-point motion and tunnelling do not play a key role. Important exceptions are molecules involving hydrogen bonding, including water, proton sponges, organic acids, and some enzymes. Quantum nuclear effects are revealed by isotope substitution experiments where hydrogen is replaced by deuterium.
I will introduce a simple model for hydrogen bonding [1] based on a two-dimensional electronic Hilbert space that gives potential energy surfaces that can be used to calculate the quantum vibrational states of the shared proton/deuterium. This leads to a quantitative description of experimental data for bond lengths, vibrational frequencies, and isotope effects for a diverse range of chemical compounds [2].

[1] R.H. McKenzie, Chem. Phys. Lett. 535, 196 (2012).
[2] R.H. McKenzie, C. Bekker, B. Athokpam, and S.G. Ramesh, J. Chem. Phys. 140, 174508 (2014).

Here are the current version of the slides for the talk.
Comments welcome.

To make things more interesting I am going to follow David Mermin's suggestion and read from some referee reports I received about this work. I once heard Mermin do this is in a talk on quasi-crystals. It was very interesting because one of the referees was Linus Pauling!