About a decade ago sodium cobaltate [NaxCoO2] was the "flavour of the month" when it came to strongly correlated electron materials. And then along came the iron pnictide superconductors....
The cobalt ions within a layer of the crystal structure form a triangular lattice and the sodium ions donate electrons to conducting layers. Hence, it is natural to consider a doped Hubbard model on a triangular lattice as the simplest possible effective Hamiltonian for these materials.
This led to numerous studies of this model. Today most studies of this model will also claim relevance to sodium cobaltates. I disagree.
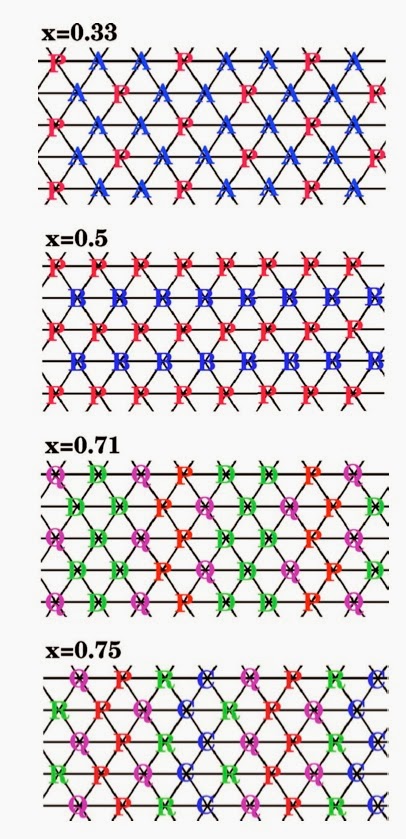
The sodium ions play a larger role that cannot be neglected. They actually modify the intra-layer electronic structure. Specifically, they spatially order in a manner dependent on the doping level.
This is unlike the case of the cuprates where the atoms between layers [and dopants] are merely spacers and do not change with doping.
Jaime Merino, Ben Powell, and I discussed this in a series of papers, discussed in an earlier post. In a 2006 PRB we considered the simple one band Hubbard model and pointed out that it could not describe all the cobaltates properties. The figure below shows how the spatial ordering of the sodium ions at different dopings produces different site energies on the triangular lattice.
No comments:
Post a Comment