Characteristics of optimal doping in cuprates

In the cuprate superconductors there is a value of the doping at which the superconducting transition temperature is a maximum (optimal doping). Coincidentally (?) this also seems to the doping at which the metallic phase is most non-Fermi liquid like. Some theories (especially due to Varma) try and connect these two phenomena via a quantum critical point below the superconducting dome. An earlier post discusses how the entropy is maximal and the thermopower changes sign near optimal doping.

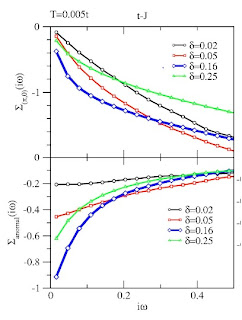
A cluster DMFT (Dynamical Mean-Field Theory) calculation by Kristian Haule reproduces the correlation between high-Tc and anomalous metallic properties. The figure below shows the Matsubara frequency dependence of the imaginary part of the self energy (at wave vector (0,pi) = anti-nodal region) (top) and the anomalous self energy (related to the superconducting pairing) for different dopings.

In a simple Fermi liquid the slope of the upper curve at low frequencies is related to the quasi-particle weight.
Haule concludes the quasi-particles are most incoherent and the scattering rate the largest around optimal doping.