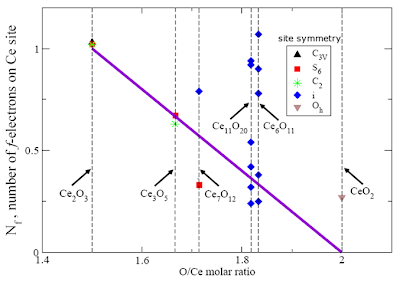
One of my students, Elvis Shoko has just submitted his Ph.D thesis, entitled "A minimal model Hamiltonian for strong electron correlations in cerium and its oxides".
Well done, Elvis!
We welcome any feedback.




Today both biology teaching and research is driven by a paradigm: first determine the biomolecular structure, then deduce the relevant properties of the structure, and then explain the function of the biomolecule.In the 21st century biology is moving away from a preoccupation with molecular biology to systems biology. Since this involves emergent properties the actual details of biomolecular structures are less important than the collective properties that they have as they interact with one another.
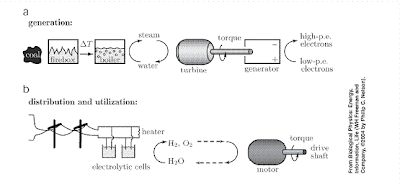
However, historically this is NOT how biology has operated, and Nelson illustrates this nicely when considering the case of molecular ion pumps and the mitochondria. One starts with a knowledge of the biological function, e.g., energy production and distribution, and one then deduces what physical property the system must have (e.g., the ability to maintain a non-equilibrium concentration gradient of ions), and one then makes a hypothesis about what kind of structure is necessary to have this property (e.g., an ion pump embedded in the cell membrane wall).

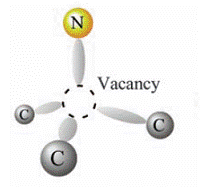 The past few years have seen significant advances in using NV (Nitrogen Vacancy) centres in diamond as qubits. A helpful review by Wrachtrup and Jelezko is here.
The past few years have seen significant advances in using NV (Nitrogen Vacancy) centres in diamond as qubits. A helpful review by Wrachtrup and Jelezko is here.








 Figure b above shows how the amount of unfolded RNA as a function of applied force can be fit simply that predicted for a two-state equilibrium distribution (which has the same mathematical form as a Fermi-Dirac distribution!) The fit also gives a good estimate of the free energy of unfolding (about 80 k_B T at room temperature).
Figure b above shows how the amount of unfolded RNA as a function of applied force can be fit simply that predicted for a two-state equilibrium distribution (which has the same mathematical form as a Fermi-Dirac distribution!) The fit also gives a good estimate of the free energy of unfolding (about 80 k_B T at room temperature).
In honour of International Women's Day, I bring to your attention a fascinating recent piece in The Conversation , Who was Amelia Frank?...
