The power of simple free energy arguments

I love the phase diagram below and like to show it to students because it is so cute.

However, in terms of understanding, I always found it a bit bamboozling.

On monday I am giving a lecture on phase transformations of mixtures, closely following the nice textbook by Schroeder, Section 5.4.

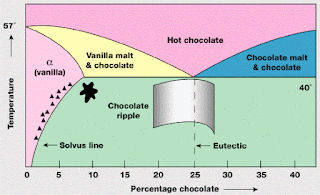
Such a phase diagram is quite common.
Below is the phase diagram for the liquid-solid transition in mixtures of tin and lead.

Having prepared the lecture, I now understand the physical origin of these diagrams.

Eutectic [greek for easy melting] point is the lowest temperature at which the liquid is stable.

What is amazing is that one can understand these diagrams from simple arguments based on a very simple and physically motivated functional form for the Gibbs free energy that includes the entropy of mixing.

It is of the form

G(x) = C + D x + E x(1-x) + T [xlnx + (1-x)ln(1-x)]

where x is the mole fraction of the one substance in the mixture and T is the temperature.
The parameters C, D, and E are constants for a particular state.

The second term represents the free energy difference between pure A and pure B.
The third term represents the energy difference between A-B interactions and the average of A-A and B-B interactions. [I am not sure this is completely necessary].
The crucial last term represents the entropy of mixing (for ideal solutions).

Below one compares the G(x) curves for the three states: alpha (solid mixture with alpha crystal structure), beta, and liquid in order to construct the phase diagram.