What is your intuition about the shear viscosity of a simple fluid?
Suppose that the mean-free path of the particles increases (e.g. due to a decrease in density, pressure, or temperature).
Would you expect the viscosity to increase or decrease?
Surely, the less collisions (as the mean-free path increases) the less the "stickiness" of the fluid.
However, it is not so simple.
Long ago Maxwell showed that for a dilute gas that the viscosity eta increases linearly with the mean-free path (which is proportional to the the self-diffusion constant D) and eta is independent of the density. A more rigorous derivation was given by Chapman and Enskog's solution of the Boltzmann equation. The exact relation is
where rho is the density and C(T)=0.83 for hard spheres. This is also what one finds for a Fermi liquid (which makes sense since it involves weakly interacting quasi-particles with long mean-free paths).
However, in the dense limit, one finds that the Stokes-Einstein relation holds
where R is the size of a molecule and c a constant of order 1.
Now, the viscosity is inversely proportional to the mean-free path, more in keeping with most people's intuition: the greater the collisions the greater the "stickiness" of the fluid.
How does one understand this crossover?
A paper by Rah and Eu is helpful. They point out how the viscosity has two contributions, the first from the kinetic energy and the second from the inter particle potential. They derive an expression for the total viscosity:
which captures both dilute and dense regimes.
I wrote this because in the luxury journal Science this week there are three experimental papers about the viscosity of the electron fluid in crystals. I found the first paragraph of one paper to be quite confusing. It seems to suggest that some of the issues above are unique to the electron fluid in a crystal and related to subtle issues about different kinds of scattering.
I welcome any insights about these subtle issues.
Subscribe to:
Post Comments (Atom)
Thermodynamics and emergence
Novelty. Temperature and entropy are emergent properties. Classically, they are defined by the zeroth and second laws of thermodynamics, re...
-
Is it something to do with breakdown of the Born-Oppenheimer approximation? In molecular spectroscopy you occasionally hear this term thro...
-
Nitrogen fluoride (NF) seems like a very simple molecule and you would think it would very well understood, particularly as it is small enou...
-
I welcome discussion on this point. I don't think it is as sensitive or as important a topic as the author order on papers. With rega...


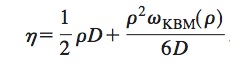


Nice post, I never realized that the shear viscosity behaves kind of counter intuitively for the dilute gas!
ReplyDelete