Spin liquid state in the spin-1 Kagome antiferromagnet

There is a nice paper
Plaquette-triplon analysis of a trimerized spin-1 Kagomé Heisenberg antiferromagnet 
Pratyay Ghosh, Akhilesh Kumar Verma, Brijesh Kumar

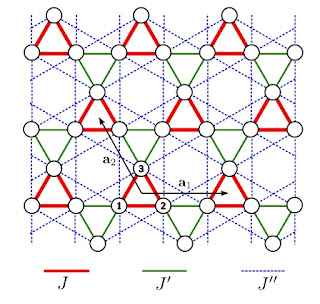
They consider an antiferromagnetic Heisenberg model on the Kagome lattice with three different interactions, J, J', and J'', shown below.

The case J'=J and J''=0 is the regular Kagome lattice model.

For J'=J''=0 one has isolated triangles for which the ground state is a singlet with an energy gap to three low-lying triplet states.
[Aside: for a nice general treatment of such triangles (and tetrahedrons) see this paper].
This state is the starting point for an analysis using bosonic excitations corresponding the triplet excitations on the triangular plaquette.
The calculated phase diagram is below.

 

One sees that turning on the inter triangle interaction J' has no effect on the quantum numbers or symmetry of the ground state. It remains a singlet, with no spontaneously broken symmetry, with an energy gap to the lowest lying triplet, i.e. a spin liquid. 

I found this surprising and interesting. But, it is also consistent with some numerical work, such as a recent DMRG study by Changlani and Lauchli. 

Only when one turns on the further frustrating next nearest neighbour interaction (J'') does one obtain a different ground state. Furthermore, a relatively small value of J''/J less than 0.2 is sufficient.

For a discussion about a possible spin liquid grounds state in the spin-1/2 Kagome model, see the suggested reading in an earlier post.

I thank the authors for helping me understand the paper.