If there is an order parameter, what is it?
Consider a single band Hubbard model at half-filling.
As U/t increases there is a transition from a metal to an insulator.
The critical value of U/t is non-zero except for cases (e.g. one dimension or the square lattice) where there is perfect Fermi surface nesting of the metal state.
Here is one picture of the transition: the metal to insulator transition is due to binding of holons and doublons. This is advocated by Yokoyama and collaborators and summarised in the Figure below (taken from this paper). At half filling there are equal numbers of holons and doublons.
In the metallic state (left) the holons and doublons are mobile. In the insulating state (right) holons and doublons are bound together on neighbouring sites.
Evidence for this picture comes from numerical simulations. Yokoyama, Ogata, and Tanaka consider the following variational wave function.
P_G is a partial Gutzwiller projection
A Monte Carlo treatment gives the graph below for the variational parameter mu as a function of U/t.
Clearly near the critical U there is a large discontinuous change in mu, reflecting a large change in the nearest neighbour correlations of holons and doublons.In contrast, at the transition there is only a small change in the variational parameter g, reflecting the fact that at the transition there is only a small change in the double occupancy [doublon density].
A recent preprint by Sato and Tsunetsugu reports investigations of the Hubbard model on the triangular lattice using cluster DMFT. The figure below shows how P^dh, the probability of a doublon and holon being on neighbouring sites (normalised to the product of the density of holons and that of doublons), changes significantly at the transition. In contrast, there are only small changes in the doublon density (shown in the inset).
A slave boson theory of the holon-doublon binding transition has recently been given by Sen Zhou, Yupeng Wang, and Ziqiang Wang.
What are some alternative pictures for the Mott transition?
Slater
The transition arises due to Fermi surface nesting and the insulating state is associated with the opening of a band gap due to new commensurability's associated with antiferromagnetic (or spin-density wave) order. Importantly, the insulator requires magnetic order.
This is a weak-coupling picture.
Brinkman-Rice
[equivalent to slave bosons = Gutzwiller approximation on a Gutzwiller variational wave function]
As U increases the band width is renormalised until it (and the double occupancy) shrinks to zero at the transition. This is a second-order transition. No magnetic order is required for the insulator.
Dynamical-mean field theory
I find this hard to summarise. Interactions produce lower and upper Hubbard bands. Self-consistent stabilisation of the metal is associated with Kondo screening of local moments by the bath of delocalised electrons, leading to a coherent band near the chemical potential. The spectral weight in this band shrinks with increasing interaction U. The transition is first order. No magnetic order is required for the insulator. This is a completely local picture.


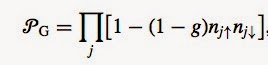





Thanks for your interesting post !
ReplyDelete