Generally it is a lot easier to numerical calculations in imaginary time than in real time. A Fourier transform then gives the value of correlation functions at
Matsubara frequencies. It then becomes a challenge to analytically continue to real frequencies. For results with little numerical noise the most widely used method is
Pade approximants, as introduced by
Vidberg and Serene. For results with statistical noise (e.g. from a quantum Monte Carlo simulation) a common approach is to use Maximum entropy methods, as
reviewed by Jarrell and Gubernatis.
In a Fermi liquid the quasi-particle weight Z is related to the real part of the self energy Sigma'(omega) by
How does one get this from the self energy at imaginary frequencies i omega_n?
It turns out one does not have to do the analytic continuation.
There is an exact identity one can use, as described in this
paper, by Arsenault, Semon, and Tremblay.
[Minor correction: the Sigma in the middle of (12) should be Sigma'', the imaginary part.]
I had never seen this before and think it is very elegant.
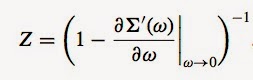




Don't you still have to analytically continue in the Matsubara frequency, which you only know at discrete values?
ReplyDeleteAusten,
ReplyDeleteGood question. You are correct that on the imaginary axis the function is only known at discrete values. One must assume a smooth interpolation between them. But, this is much better controlled than continuing to the real axis.
I was a bit loose with using -> 0 and = 0 for real frequency but since the self-energy is well behave around w = 0 in the Fermi liquid regime there is no problem.
ReplyDeleteHowever, the arrow in w_n -> 0 in Eq.12 is important because formally when we do it numerically, it is an extrapolation. The derivation is correct (You are indeed right concerning the typo of Eq.12. I saw it recently when I wanted to copy-paste the equation.), but w_n -> 0 would only be true for Fermions at zero temperature, which cannot be the case if we do the calculation on the imaginary axis. Thus, it is indeed an extrapolation that enable one to get an estimation without having to do the analytical continuation.
There are many ways we could choose to do it and by far, we were not the first to use this approximation, it is very popular in the DMFT literature. Although, I never saw the proof given and I may very well have missed a paper where it is, but I thought it might be a good idea to put it in our paper so if others are looking for that proof, it is there.
For the numerical calculation, for example the simplest way to find the answer would be to take the self-energy for a calculation at very low temperature, a T for which we are in the FL state (since DMFT gives a FL at low T) and consider that since the self-energy of a Fermi liquid should be dominantly linear in w_n for low w_n, simply taking Im[Sigma(w_0)]/w_0 is the right approximation. Another popular way and the one we used, is to get Im[Sigma(w_0)]/w_0 for few very low temperatures (all the other parameters fixed of course) and extrapolate to T = 0. If we have a Mott insulator, of course the choice does not matter since we are not in a FL state and the self does not go to zero as w_n -> 0, but we of course obtain Z approx 0 which is the right approximation of Z = 0.
Therefore yes, formally, to find something like Z (contrary to the density or energy for example) we would need analytical continuation since w_n -> 0 is not possible at finite T, but at small enough T, this is a very good approximation.
This is also something similar when we use G(tau = beta/2) as an approximation for the density of states at the Fermi level i.e. A(0). This is fine at low enough T.