Back of the envelope estimates in chemistry
Michelle Francl has a stimulating piece Take a number: Back-of-the-envelope calculations are an important part of chemistry in Nature Chemistry.
Francl asks her students, "Estimate the circumference of a benzene ring in metres".
This is an example of a Fermi problem.
Previously I posted about the importance of teaching solid state physics in a way that helps students get a feel for orders of magnitude. I don't think I could write a comparable post for physical chemistry. This is partly my lack of expertise and experience, but also I suspect that things in chemistry are not as clear. [One day I hope I will get asked to teach a course.]
For example, one thing I learnt and need to understand is that X-H bonds are shorter than X-X bonds.
Indeed, Francl says
Well, one of my own personal favourites is anchoring chemical timescales. From 10-18 s (that of electron dynamics, and presumably the fastest processes in chemistry) to 10+18 (approximately the age of the universe). And (for a unimolecular process) this can be reduced to this equation:
Ln(k/T) = 23.76 – ΔG‡/RT
I quoted this equation in a recent post, since it gives you the fastest possible chemical reaction if ΔG‡ is set to zero (which of course is not a reaction but a vibration), but which gives you a good estimate of how fast a process will be for any given value of a barrier.
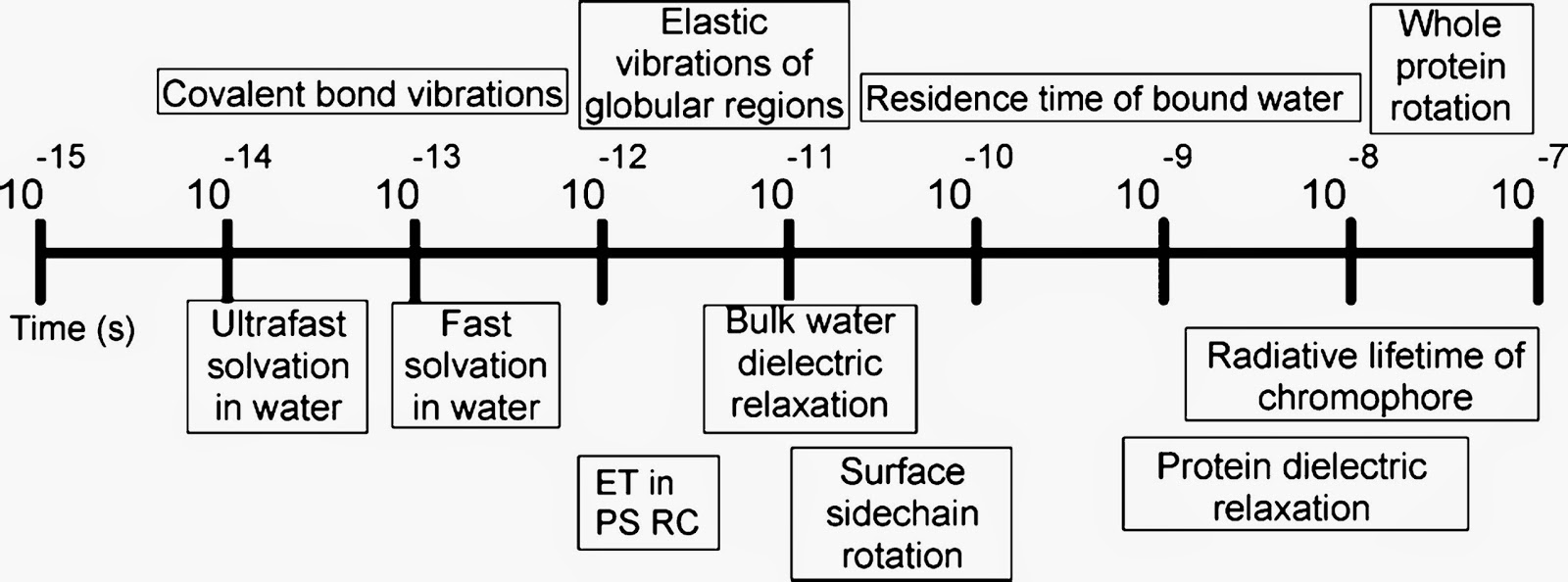
When it comes to condensed phase dynamics there are a multitude of different timescales, summarised in diagram below, taken from this review.
For me remembering that at room temperature, k_B T = 25 meV = 0.6 kcal/mol = "chemical accuracy" is useful. Basically, most electronic energy scales (ionic and covalent bond energies, energy barriers = activation energies) are of the order of eV. You see this in that most batteries [electrochemical cells] have voltages of a few volts.
What do you think are key orders of magnitude in chemistry?
Francl asks her students, "Estimate the circumference of a benzene ring in metres".
This is an example of a Fermi problem.
Previously I posted about the importance of teaching solid state physics in a way that helps students get a feel for orders of magnitude. I don't think I could write a comparable post for physical chemistry. This is partly my lack of expertise and experience, but also I suspect that things in chemistry are not as clear. [One day I hope I will get asked to teach a course.]
For example, one thing I learnt and need to understand is that X-H bonds are shorter than X-X bonds.
Indeed, Francl says
I recently asked a few hundred of my closest chemical friends on Twitter and Facebook what should go on such a sheet for chemists, what they might encourage students to master. Schematics of periodic trends and the electromagnetic spectrum are obvious candidates for mappings, but the list of suggested anchors varied wildly with subfield. There are very few values that a majority of chemists cling to: room temperature is 300 K; the length of a single carbon–carbon bond is 154 pm; the atomic masses of C, H, N, O, S and Cl.In response to Francl's article, Henry Rzepa says
Well, one of my own personal favourites is anchoring chemical timescales. From 10-18 s (that of electron dynamics, and presumably the fastest processes in chemistry) to 10+18 (approximately the age of the universe). And (for a unimolecular process) this can be reduced to this equation:
Ln(k/T) = 23.76 – ΔG‡/RT
I quoted this equation in a recent post, since it gives you the fastest possible chemical reaction if ΔG‡ is set to zero (which of course is not a reaction but a vibration), but which gives you a good estimate of how fast a process will be for any given value of a barrier.
When it comes to condensed phase dynamics there are a multitude of different timescales, summarised in diagram below, taken from this review.
For me remembering that at room temperature, k_B T = 25 meV = 0.6 kcal/mol = "chemical accuracy" is useful. Basically, most electronic energy scales (ionic and covalent bond energies, energy barriers = activation energies) are of the order of eV. You see this in that most batteries [electrochemical cells] have voltages of a few volts.
What do you think are key orders of magnitude in chemistry?

Comments
Post a Comment