Here is my tentative answer motivated by strongly correlated electron materials.
A key signature of strong correlations is a significant redistribution of spectral weight [i.e., the many-body eigenvalue spectrum] compared to the corresponding non-interacting electron problem.
Common phenomena associated with this redistribution are
- the emergence of new low-energy scales [e.g. Kondo temperature]
- large renormalisation of quasi-particle energies [heavy fermions]
- separation of the energy scales for spin and charge excitations
- incoherent spectral features [Hubbard "bands"]
- breakdown of quasi-particle approximations [bad metals]
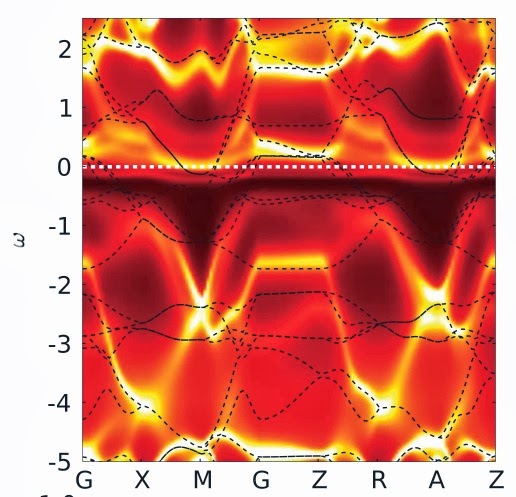
I attempt to illustrate this idea with two figures below. The first color shaded plot shows the one-particle spectral density calculated from LDA+DMFT [Local Density Approximation for DFT (Density Functional Theory) + Dynamical Mean-Field Theory] for the parent compound of the iron pnictide superconductors.
The dashed lines are the band structure calculated from pure LDA [i.e. not including the strong correlation effects captured by DMFT].
The Figure is taken from a PRL by Haule, Shim, and Kotliar.
The figure below shows the spectral density measured by ARPES [Angle Resolved PhotoEmission Spectroscopy] for the iron pnictide LaOFeP. The solid red lines are the band structure calculated from LDA.
This is Figure 6 in a recent review from Z.X. Shen's group.
In the absence of strong correlations all of the spectral weight would lie on top of the band structure.
The important point is that it does not.
In the cuprates these effects are even more dramatic.
So what about cold atomic gases?
For fermionic systems I have not seen much discussion of redistribution of spectral weight.
Often a quasi-particle picture and mean-field techniques are used in theoretical calculations.
Chris Vale's group has done a beautiful series of experiments measuring dynamical spin and density correlation functions for a strongly interacting system with a BEC-BCS crossover. The figure below is taken from this PRL. One does see differences between the density [D] and spin [S] correlation functions and there is a redistribution of spectral weight. But, to me at least, it does not appear as dramatic as in strongly correlated electron materials.
For bosons near the Mott transition there has been some discussion of the spectral weight redistribution [see this PRA and references therein].
I think the condensate fraction in the first cold atom BEC's is close to unity. In contrast, in superfluid helium 4 the fraction is about 10 per cent. The vanishing of the condensate fraction as one approaches the Mott insulator has been observed, but seems to be captured by a mean-field theory.
For reference, in cuprate superconductors the superfluid density can be much less than the charge density.
So, my questions are:
Is large redistribution of spectral weight the best signature of strong correlations?
In what cold atom systems does one see the largest redistribution?




>Is large redistribution of spectral weight the best signature of strong correlations?
ReplyDeleteI think this is an excellent starting definition. But if we want to be pendantic, its important to specify clearly what non-interacting version of the same problem you are referencing to. For instance, its not necessarily clear what to compare to when you are asking about whether magnetic system are strongly correlated or not. Or superconductors. In the former case perhaps the reference state should be some system described by some sort of linearized spin-wave theory. But spin waves are of course far from the bare electrons that make them up etc. etc.
Your definition is a good one, because I think its important to point out that a distinguishing feature of strong correlations is not necessarily "strong interactions". Interactions are always of the same order as the kinetic energy in a bound system through the virial theorem. But some class of these interactions can typically be taken into account in a fashion that turns them into an effective kinetic energy or in a mean-field fashion. The former case is for instance what happens in band theory of electrons.
Hi Peter,
DeleteThanks for the comment.
I agree that my proposal is not clear cut and am glad it is generating some discussion.
I was taking the reference to be non-interacting electrons. By this criteria any magnetic system associated with a Mott insulator is strongly correlated. But, as you point out, the spin excitations may still be "boring" and captured by some quasi-particle/semi-classical picture such as linear spin wave theory.
I mostly agree with Peter: one needs to specify the standard mean-field theory to say whether the system is strongly correlated or not.
ReplyDeleteTake the Mott transition is the Bose-Hubbard model. The standard mean-field approach for bosons is Bogoliubov theory, that completely fails to find the transition, which is driven by the strong on-site correlations. One would thus say that that's a strongly correlated system.
But of course, another mean-field like approach, such as the strong-coupling RPA (that takes the on-site physics into account exactly) captures most of the physics of the Mott transition. According to you criterion, it is not a strongly correlated system...
As a side remark, the Mott transition in 2D, at the tip of the Mott lobes, is described by the quantum O(2) model in (2+1)D, which is a strongly correlated theory (no quasi-particles, non-trivial critical exponents, etc.). That's what makes the study of the amplitude (""Higgs"") mode close to the critical point so interesting and challenging.
Adam
Hi Adam
DeleteThanks for the helpful comment.
I stress my main criterion is not whether some sort of mean-field theory works.
Rather, it is major redistribution of spectral weight. According to some of the papers I referenced it looks like there is such a redistribution near the Mott insulator-superfluid transition for bosons.
Hi,
Deletethe thing is, major redistribution has to be compared to a reference state, that can be in principle anything.
If I understand correctly your reply to Peter's comment, you compare to the free electron case. But then, superconductivity implies a major change compare to free electrons, the same way that the spectral weight is completely changed in weakly interacting condensed bosons. But that's not what you would call strongly correlated, wouldn't you?
I think it is an interesting question, especially since people tend to use the term in a very broad sense, and as Peter said, people tend to confuse strongly interacting with strongly correlated.
I should clarify something for the above discussion.
ReplyDeleteI do NOT classify a conventional superconductor [i.e. BCS, lead, tin, ...] as strongly correlated. There is a redistribution of spectral weight, but it is all at low energies much less than the Fermi energy [and conduction band-width].
In contrast, in the metallic phase of the cuprates, organics, pnictides, the spectral weight is redistributed on scales comparable to band width that one gets from an LDA [i.e. weakly interacting electrons] calculation.
I think it is a good proposed definition (especially as regards the applicability of quasiparticle dynamics) because neither strongly-correlated nor strongly-interacting implies the other, and it is helpful to distinguish the two.
ReplyDeleteAs for the second question; I'm not sure exactly which system has the largest redistribution of spectral weight, but the 1-dimensional Bose gas (Lieb-Liniger model) certainly has a redistribution, and is worth thinking about.
ReplyDeleteThe many-body eigenvalues map over from an ideal-Bose to an ideal-Fermi system with the tuning of a Feshbach resonance, or using a confinement-induced resonance.
Would you consider this redistribution to be "significant"? I personally think it is, because, in relation to the non-interacting system, the spectrum is completely altered. Of course, the fact that the nature of its alteration, is to look exactly like an ideal Fermi gas means that you could understandably contest; "it's only as strongly correlated as the statistical correlations in an IDEAL Fermi gas!"