Physicists like effective Hamiltonians such as the Hubbard, Heisenberg, and Anderson models. Why do they work so well? What do the parameters in the Hamiltonian actually correspond to? How are the orbitals related to atomic and molecular orbitals?
These days, computational chemists are not so enthusiastic about such semi-empirical theories.
Today I read through a nice article, Is There a Bridge between ab Initio and Semiempirical Theories of Valence?, by Karl Freed.
It describes a strategy for partitioning the full Hilbert space into two parts P and Q, where P is the space of configurations involving only valence electrons.
The key equation (8) gives an exact expression for the valence Hamiltonian [which acts only on the space of states P] in terms of the full Hamiltonian.
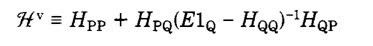
He then explicitly evaluates the Hamiltonian matrix elements for small atoms and molecules. The values are consistent with experiment but significantly different from those evaluated at the Hartree-Fock (self-consistent field) level.



In a nutshell Freed block-diagonalizes the Hamiltonian to separate the valence
ReplyDeletepart of the Hilbert space from the rest.
Strictly, this is only possible for finite systems (eigenvalue problem).
Yet, often, a similar procedure (Löwdin downfolding, J. Chem. Phys. 19, 1396) is employed for the one-particle part
of the Hamiltonian of extended systems. Indeed, in a field description, integrating out the "Q" degrees of freedom
(considered to be of one-particle type only) yields an effective action of the PP-sub-system with an effective propagator
$\widetilde{G}_{PP}^{-1}=(G^{-1})_{PP}+H_{PQ}(\omega-H_{QQ})^{-1}H_{QP}$ -- in stark resemblance to Freed's eq (8).
An approximate effective Hamiltonian for the PP-subspace can be obtained by linearizing the frequency dependence at
the energies of the bands that have been integrated out, therewith recovering eq (8).
In the likely case that the P and Q degrees of freedom are coupled by interactions (two-particle terms), this procedure
might not capture all the physics even at low energies.
For a recent scheme that includes those couplings in the construction of an effective self-energy for a sub-space of orbitals,
I humbly suggest to have a look at PRL 102, 176402.