Something amazing about Einsteinian gravity

When I read Fundamentals by Frank Wilczek I learnt something that I found beautiful and amazing about general relativity and quantum field theory.

Any massless spin-2 field must couple to the stress–energy tensor in the same way that gravitational interactions do. This is an alternative means to derive Einstein's equation.

Furthermore, if a massless spin-2 particle is discovered, it must be the graviton. There is a nice discussion of this on physics.forums

According to Wikipedia, "For a comparison of the geometric derivation and the (non-geometric) spin-2 field derivation of general relativity, refer to box 18.1 (and also 17.2.5) of Misner, C. W.; Thorne, K. S.; Wheeler, J. A. (1973). Gravitation." 

In the 1960s, Steven Weinberg published a series of seminal papers, summarised below by one commenter in the physics.forums discussion. The results are also derived in chapter 5 of Weinberg's Quantum Field Theory text (volume 1).

S. Weinberg, “Photons and gravitons in S-matrix theory: derivation of charge conservation and equality of gravitational and inertial mass,” Phys. Rev. 135, B1049 (1964). 

S. Weinberg, “Photons and gravitons in perturbation theory: Derivation of Maxwell’s and Einstein’s equations,” Phys. Rev. 138, B988 (1965). 

S. Weinberg, “Infrared photons and gravitons", Phys. Rev. 140, B516 (1965).

1) Maxwell’s theory is the most general Poincare’ and gauge invariant theory of massless spin-1 particle. This can be easily proved by writing down the most general Poincare invariant amplitude for emitting a single photon in the so-called soft limit. Then, by demanding gauge invariance, you get charge conservation. 

2) Einstein’s GR is the most general Poincare’ and generally covariant theory for a massless spin-2 particle. The proof is similar to photon case. You write the most general amplitude for emitting a soft graviton. Then you see what happens when you demand general covariance, i.e., demand that the amplitude is “gauge” invariant. If you do that, you find that the equivalence principle pops out. That is, all particles couple to the massless spin-2 particle with equal strength. From this, he also concluded that the coupling strength must vanish when the spin of the massless particle is greater than 2. To some extent, this explains why we don’t see this kind of particle. 

3) Yang-Mill’s theory is the most general Poincare’ and gauge invariant theory for massless, self-interacting spin-1 particles. In this case, if you do the same exercise, you find that the coupling strengths of the interaction satisfy the Lie algebra of a compact group.

It is fascinating that these papers were just a warm-up for Weinberg's 1967 electro-weak unification paper, "A model for leptons" which is the basis of his Nobel Prize, and the most cited PRL ever.

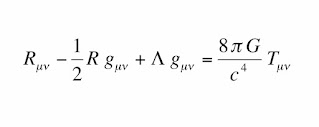
Comments

Post a Comment

Popular posts from this blog

Is it an Unidentified Superconducting Object (USO)?

If you look on the arXiv and in Nature journals there is a continuing stream of people claiming to observe superconductivity in some new material. There is a long history of this and it is worth considering the wise observations of Robert Cava , back in 1997, contained in a tutorial lecture. It would have been useful indeed in the early days of the field [cuprate superconductors] to have set up a "commission" to set some minimum standard of data quality and reproducibility for reporting new superconductors. An almost countless number of "false alarms" have been reported in the past decade, some truly spectacular. Koichi Kitazawa from the University of Tokyo coined these reports "USOs", for Unidentified Superconducting Objects , in a clever cross-cultural double entendre likening them to UFOs (Unidentified Flying Objects, which certainly are their equivalent in many ways) and to "lies" in the Japanese translation of USO.   These have caused g
Read more

What is Herzberg-Teller coupling?

Image
Is it something to do with breakdown of the Born-Oppenheimer approximation? In molecular spectroscopy you occasionally hear this term thrown around. Google scholar yields more than 3000 hits. But I have found its precise meaning and the relevant physics hard to pin down. Quantum mechanics in chemistry by Schatz and Ratner is an excellent book , but the discussion on page 204 did not help me. "Herzberg-Teller" never appears in Atkins' Molecular quantum mechanics. So here is my limited understanding. Herzberg and Teller wanted to understand why one observed certain vibronic (combined electronic and vibrational) transitions that were not expected, particularly some that were expected to be forbidden on symmetry grounds. " Intensity borrowing " occurred. Herzberg and Teller pointed out that his could be understood if the dipole transition moment for the electronic transition depended on the nuclear co-ordinate associated with the vibration. In the Franck-Condo
Read more

What should be the order of authors on a conference poster or talk?

I welcome discussion on this point. I don't think it is as sensitive or as important a topic as the author order on papers. With regard to paper authorship my general rule is that the person who does the bulk of the work, including actually writing the paper should be the first author. Doug Natelson has a good post on co-authorship , that I largely agree with. My only difference is that I am not really convinced that good practice prevails in the majority of circumstances. I fear there are increasing numbers of co-authors, particularly senior ones, with marginal contributions. But, what about conference talks and posters? Many of these are based on work that is already or about to be published. Should the author order be identical as the associated papers? I am not sure it should necessarily be. My tentative view is that the person who writes and submits the abstract and actually prepares and presents the post/talk should be the first author. Perhaps they should also highlig
Read more