An important question about emergent properties is whether they can be explained solely in terms of the properties of the components of the system. Here I explore the question from the point of view of Hempel's covering law of scientific explanation, discussed in my last post.
According to Hempel, a scientific explanation E of a specific phenomena P is a logical argument that starts with some premises, at least one of which is a scientific law L, and which logically implies P.
I now give a version of this that describes a microscopic scientific explanation of some emergent property.
Suppose that a macroscopic system S has property X. S is composed of many interacting microscopic components whose properties, including their interactions, have a finite enumeration x1, x2, x3,...xn. None of these properties is X. Hence, in the sense of novelty, X is an emergent property of S. Let l1, l2, l3,.., lm be a finite number of microscopic laws. Then X has a microscopic scientific explanation if it can be deduced from the x's and l's.
A possible problem with most microscopic "explanations" of emergent properties may be whether they at some point implicitly assume some "emergent" scientific law, such as spontaneous symmetry breaking, or the existence of X. Let me illustrate this possible problem with some examples.
Irreversibility. Microscopic laws are invariant under time-reversal. But macroscopic systems exhibit irreversible behaviour such as the mixing of two distinct fluids. This is encoded in the second law of thermodynamics. This problem of the "arrow of time" is nicely discussed by Tony Leggett in The Problems of Physics, in a chapter entitled "Skeletons in the Cupboard." An alternative perspective is that of Joel Lebowitz, who claims Boltzmann solved the problem.
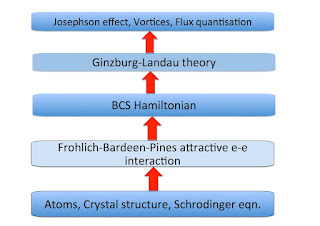
Superconductivity. One could claim that BCS theory provides a microscopic explanation of superconductivity. We start with the properties of electrons, ions, Coulomb's law, quantum mechanics, and statistical mechanics. These properties and microscopic laws can be used to show that there is an effective attractive interaction between electrons. One then considers the BCS variational wavefunction and calculates the properties of the macroscopic system. They are consistent with experimental observations of superconductivity. It is explained!
However, there are several problems on the way, which all in some sense involve assuming that superconductivity does occur. First, investigating the variational wave function only shows that the superconducting state has lower energy than the normal metallic state. This does not prove it is the true ground state. In fact, in one dimension it is not.
But potentially more fatal to the claimed microscopic explanation is that it assumes that spontaneous symmetry breaking is allowed, including (in some subtle sense that people still argue about) the breaking of the gauge symmetry of electromagnetism. One of the major points that Phil Anderson was trying to make in More is Different is that spontaneous symmetry breaking is a law of nature that should be viewed as of similar status to microscopic laws such as Schrodinger's equation.
Mean-field theory of antiferromagnetism. One might claim that one can start with a classical Heisenberg or Ising model, and classical statistical mechanics, crank the mathematical handle and get antiferromagnetic. If one does mean-field theory, then one is not really doing statistical mechanics as one is considering a weird ensemble and a Hamiltonian that is no longer microscopic. Suppose instead one does the exact solution of the Ising model. That can give the magnetic state and all the critical exponents. But, it is not clear to me that when one takes the thermodynamic limit, one assumes that the broken symmetry state is allowed. Similar questions arise for me if one does a computer simulation on large lattices and uses clever finite-size scaling techniques to deduce physical properties of the emergent state. Does the assumption of the validity of these techniques amount to some extra (macroscopic) law of nature?
I wonder whether some of these issues would be clarified (or just muddied) by considering the Thermodynamic Formalism: The Mathematical Structure of Equilibrium Statistical Mechanics by David Ruelle. In particular, does he make clear how an equilibrium broken symmetry magnetic state is fundamentally different from the microscopic equilibrium state associated with a finite number of spins.
I welcome ideas on how to clarify these issues.




Concerning SSB, I don't think that there is any doubt that it is emergent, without needing to add it by hand as a new law. At least in some cases, like the Ising model, it can be rigorously proven that starting from the microscopic Hamiltonian, there exist a temperature below which the magnetization can take two values, depending on how the magnetic field is sent to 0. A book somewhat readable by physicist is the one by Friedli and Vilenik (https://www.unige.ch/math/folks/velenik/smbook/).
ReplyDeleteOn a less rigorous side, the exact solution of e.g. the O(N) model in the large N limit also shows that SSB can be understood starting from a purely microscopic approach. This allows one to formally understand how an infinite number of degrees of freedom leads to the emergence of long-range order.
I'd say that the entire formalism of statistical mechanics is emergent, since it argues a priori a statistical distribution of how states are occupied. Also, it is not clear a priori why a system with zero applied field should be treated as a limit with non zero-field and infinite degrees of freedom, especially since the limits do not commute. This particular choice could also be made to be "emergent" (i.e. we didn't know why to make it from microscopic properties), and thus it is equivalent to SSB as an emergent property. However I think this last part may be circumvented by looking at the correlation functions, which show a form of SSB even in the absence of an infinitesimal pinning field (something which explicitly breaks the symmetry and then goes to zero).
DeleteRoss, I think a rigorous mathematical foundation for SSB in some cases has been established. See Appendix A of https://link.springer.com/article/10.1007/BF01218021 (for AFM order in some models) and reference https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.94.080401 for a BEC state. Regards, Eduardo.
ReplyDeleteAbout SSB, I think the MFT will erase the structure that shows the importance of thermodynamics limit since it just reduce the problem back to single particle physics. The explanation I like most is when we are at the thermodynamic limit, the symmetry related sectors get divided into pieces. I found it useful to think in that way since it is very helpful to understand Elitzur's theorem. Using this approach, SSB will be considered as an emergent property because it is theoretically sharply defined only when N is send to infinity.
ReplyDelete