Quantum limits to the shear viscosity in the unitary Fermi gas

Previously, I posted about possible quantum limits to the shear viscosity in quantum many-body systems. This has attracted a lot of interest because of claims, based on string theory techniques [AdS-CFT correspondence] that there is a universal lower bound for the ratio of the shear viscosity to the entropy.

There are two interesting papers

Hydrodynamic fluctuations and the minimum shear viscosity of the dilute Fermi gas at unitarity
Clifford Chafin and Thomas Schäfer

Temperature evolution of the shear viscosity in a unitary Fermi gas 
 Gabriel Wlazłowski, Piotr Magierski, Aurel Bulgac, and Kenneth J. Roche

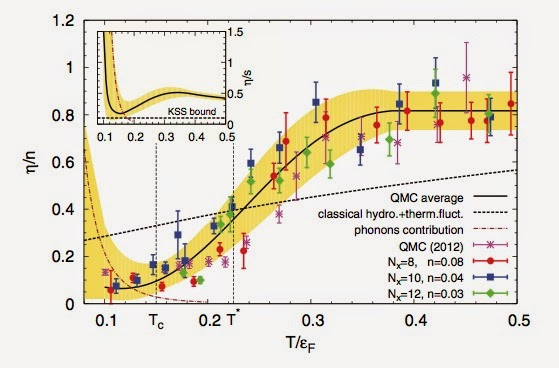
The main result of the latter is shown in the Figure below. The error bars arise because the results are based on a Quantum Monte Carlo simulation with imaginary time data that must be analytically continued to real frequencies [a thorny problem]. Tc is the superfluid transition temperature and T* the pseudogap temperature.

A few reasons why this is interesting.

1. In 1936 the legendary theoretical chemist Henry Eyring proposed a lower bound for the viscosity of n hbar, where n is the particle density. Here, we see that bound is violated.

2. The inset shows that the string theory bound is respected.

3. At low temperatures, the "classical" bound of about 0.2 n hbar, proposed in the first paper is violated.

4. The temperature dependence shows this is a strongly correlated fermion fluid, a long way from a Fermi liquid. For the latter, such as liquid 3He, the viscosity at low temperatures goes like 1/T^2, i.e. increases as the temperature decreases, and is much larger than n hbar. The fermion fluid here is something like a "bad metal" since these small viscosities correspond to mean free paths comparable to the Fermi wavelength.