Seeking definitive signatures of quantum criticality

Generally I am skeptical about quantum criticality as an important organising principle for strongly correlated electron materials (see for example, this earlier post, Are elemental metals quantum critical?). The most significant evidence is probably in heavy fermion compounds. However, particularly in the cuprates, I see quantum criticality as one of several competing "hand waiving" explainations of unusual properties. It is important to keep coming back to the idea that a true quantum critical point (QCP) will be associated with some diverging correlation length for some type of "order". Furthermore, this should lead to power laws in physical quantities over several orders in magnitude.

There is an interesting paper
Transport near a quantum critical point in BaFe2(As1−xPx)2
James G. Analytis,  H-H. Kuo, Ross D. McDonald,  Mark Wartenbe,  P. M. C. Rourke, N. E. Hussey,  and I. R. Fisher

The relevant background and context is this review article which contains the figure below

A few comments on the paper.

1. At room temperature the resistivity becomes of the order of the Mott-Ioffe-Regel limit, characteristic of a bad metal.

2. The low temperatures the metal is always a Fermi liquid [at least has a resistivity with a quadratic temperature dependence] even at dopings very close to the putative QCP. This is seen in the next figure.

3. The graph below shows the temperature dependence of the slope of the resistivity. It is striking that at high temperatures it has the approximately the same value, independent of doping. This is consistent with an earlier claim of such universality, [that even extended to elemental metals!]

4. The data above only shows a linear in T resistivity [which is often associated with quantum criticality], over less than one decade of temperature.

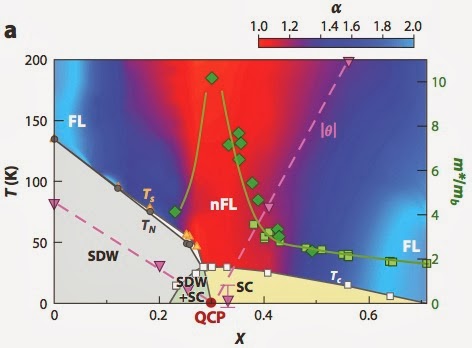
5. The figure below shows the doping dependence of the A coefficient of the Fermi liquid resistivity and the effective mass. Note the range of values of A is at most one order of magnitude. The effective mass only changes by about a factor of three.
In quantum critical theory both should diverge at the critical point [dashed line]. However, in the actual experimental data A does not diverge but decreases for the smallest x=0.31. This can be seen with the naked eye in the data above.

6. The colour shaded plot below shows the exponent n of the resistivity temperature dependence. The dashed line shows the Fermi liquid temperature going to zero at the putative QCP. However, as noted above even at the critical doping a Fermi liquid is always seen at low temperatures.

7. What about alternative theories?
One candidate must be Selective Mottness, as described in this preprint.
It does predict a significant enhancement doping dependence of the effective mass and the Fermi liquid coherence temperature. I am not sure how the P doping translates to band filling. Hopefully the proponents can comment.
Unlike quantum criticality Selective Mottness is actually based on calculations from a microscopic model with realistic interactions.