Mapping quasi-particles in strongly interacting ultra cold fermionic gases

There is an interesting preprint
Breakdown of Fermi liquid description for strongly interacting fermions 
Yoav Sagi, Tara E. Drake, Rabin Paudel, Roman Chapurin, Deborah S. Jin

It describes some nice ultra cold atom experiments that tune through the BEC-BCS crossover with a Feshbach resonance, focusing on the properties of the normal (i.e. non-superfluid) phase. All the measurements are at a temperature of T=0.2T_F, just above the superfluid transition.
It is like an ARPES [Angle Resolved PhotoEmission Spectroscopy] experiment in the solid state.
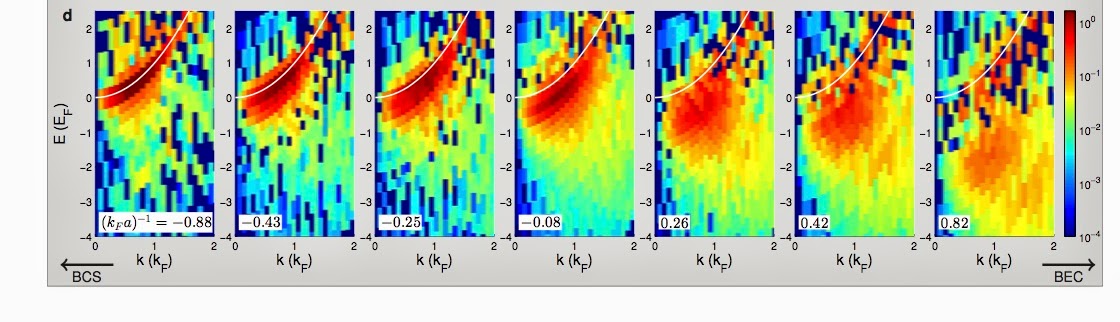
Specifically, the one-fermion spectral function A(k,E) is measured, shown in the colour intensity plots below.

The left and right side correspond to the BCS and BEC limits respectively. The unitary limit [i.e. infinite interaction occurs close to the middle].

On the left one can clearly see dispersing quasi-particle excitations, as one would expect in a Fermi liquid. As the interaction strength increases this feature is broader and there is more incoherent spectral weight at lower energies.

Some caution is in order as there is quite a bit of curve fitting involved in the analysis of the above data. [Solid state ARPES also suffers from this problem to.]

Specifically, the form below is used for the spectral function, where Z is the quasi-particle weight

In an earlier post I considered the history of this type of expression.

For the incoherent part the authors make the somewhat ad hoc assumption that it is given by a
 "function that describes the normal state in the BEC limit, namely, a thermal gas of pairs."

They then find the following results for the dependence of Z and the effective mass m* [defined by the quadratic dispersion] on the interaction strength [a is the scattering length, which becomes infinite at the Feshbach resonance, i.e. for the unitary limit].

There is already a theory paper that discusses the experiments. It captures the results above at the semi-quantitative level using a Brueckner-Goldstone theory. The self energy is assumed to be frequency independent in this approximation. I found this interesting as it is the opposite to Dynamical Mean-Field Theory (DMFT) for which the self energy is assumed to be momentum independent.

I feel the paper title may be a misnomer. The quasi-particle weight is always finite, except in the BEC regime [attractive interactions] where one does not really have fermions anymore.

In future experiments, it would be nice to see the temperature dependence of the spectral function. Specifically, do the quasi-particles get destroyed with increasing temperature as in bad metals.

I thank Matt Davis for bringing the preprint to my attention.